Tree-structured Markov random fields with Poisson marginal distributions

A new family of tree-structured Markov random fields for a vector of discrete counting random variables is introduced. According to the characteristics of the family, the marginal distributions of the Markov random fields are all Poisson with the same mean, and are untied from the strength or structure of their built-in dependence. This key feature is uncommon for Markov random fields and most convenient for applications purposes. The specific properties of this new family confer a straightforward sampling procedure and analytic expressions for the joint probability mass function and the joint probability generating function of the vector of counting random variables, thus granting computational methods that scale well to vectors of high dimension. We study the distribution of the sum of random variables constituting a Markov random field from the proposed family, analyze a random variable's individual contribution to that sum through expected allocations, and establish stochastic orderings to assess a wide understanding of their behavior.

Preventing RNN from Using Sequence Length as a Feature

Recurrent neural networks are deep learning topologies that can be trained to classify long documents. However, in our recent work, we found a critical problem with these cells: they can use the length differences between texts of different classes as a prominent classification feature. This has the effect of producing models that are brittle and fragile to concept drift, can provide misleading performances and are trivially explainable regardless of text content. This paper illustrates the problem using synthetic and real-world data and provides a simple solution using weight decay regularization.

Micro-level Reserving for General Insurance Claims using a Long Short-Term Memory Network

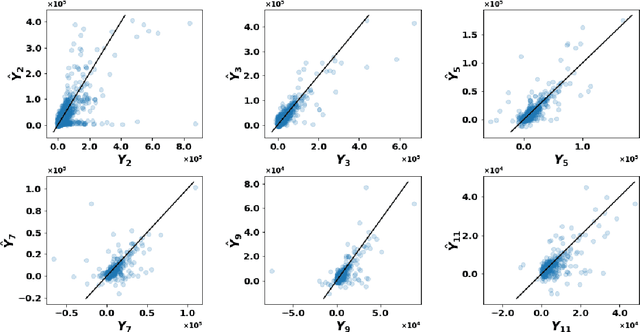
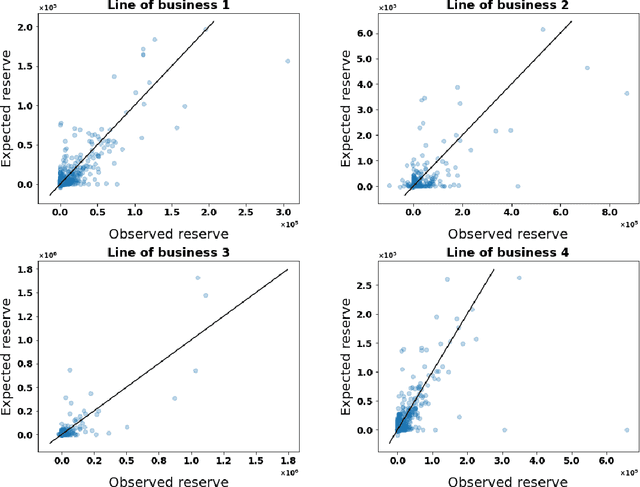
Detailed information about individual claims are completely ignored when insurance claims data are aggregated and structured in development triangles for loss reserving. In the hope of extracting predictive power from the individual claims characteristics, researchers have recently proposed to move away from these macro-level methods in favor of micro-level loss reserving approaches. We introduce a discrete-time individual reserving framework incorporating granular information in a deep learning approach named Long Short-Term Memory (LSTM) neural network. At each time period, the network has two tasks: first, classifying whether there is a payment or a recovery, and second, predicting the corresponding non-zero amount, if any. We illustrate the estimation procedure on a simulated and a real general insurance dataset. We compare our approach with the chain-ladder aggregate method using the predictive outstanding loss estimates and their actual values. Based on a generalized Pareto model for excess payments over a threshold, we adjust the LSTM reserve prediction to account for extreme payments.

Geographic ratemaking with spatial embeddings

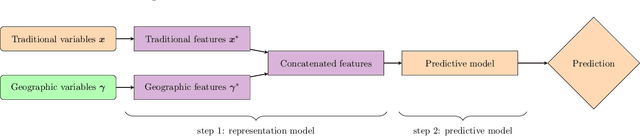
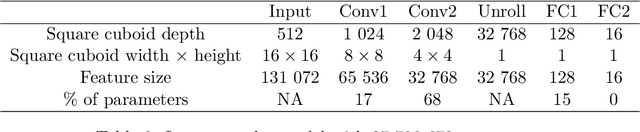
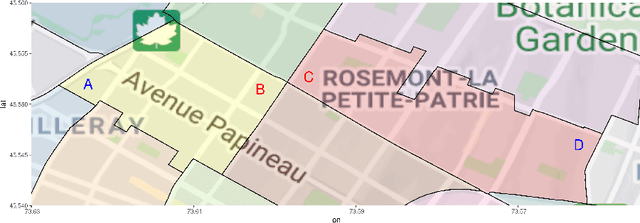
Spatial data is a rich source of information for actuarial applications: knowledge of a risk's location could improve an insurance company's ratemaking, reserving or risk management processes. Insurance companies with high exposures in a territory typically have a competitive advantage since they may use historical losses in a region to model spatial risk non-parametrically. Relying on geographic losses is problematic for areas where past loss data is unavailable. This paper presents a method based on data (instead of smoothing historical insurance claim losses) to construct a geographic ratemaking model. In particular, we construct spatial features within a complex representation model, then use the features as inputs to a simpler predictive model (like a generalized linear model). Our approach generates predictions with smaller bias and smaller variance than other spatial interpolation models such as bivariate splines in most situations. This method also enables us to generate rates in territories with no historical experience.