A review of clustering models in educational data science towards fairness-aware learning

Ensuring fairness is essential for every education system. Machine learning is increasingly supporting the education system and educational data science (EDS) domain, from decision support to educational activities and learning analytics. However, the machine learning-based decisions can be biased because the algorithms may generate the results based on students' protected attributes such as race or gender. Clustering is an important machine learning technique to explore student data in order to support the decision-maker, as well as support educational activities, such as group assignments. Therefore, ensuring high-quality clustering models along with satisfying fairness constraints are important requirements. This chapter comprehensively surveys clustering models and their fairness in EDS. We especially focus on investigating the fair clustering models applied in educational activities. These models are believed to be practical tools for analyzing students' data and ensuring fairness in EDS.

Evaluation of group fairness measures in student performance prediction problems

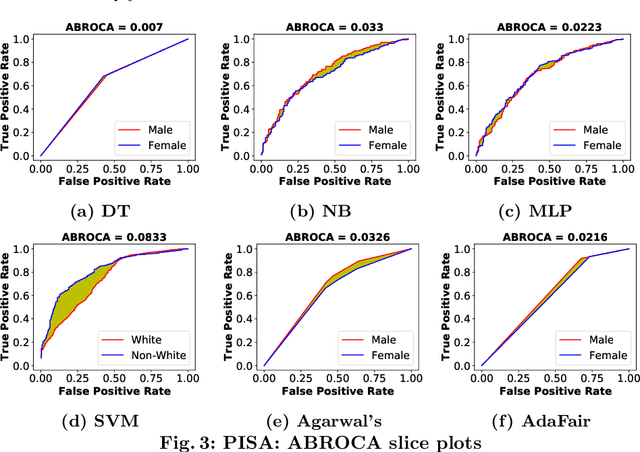
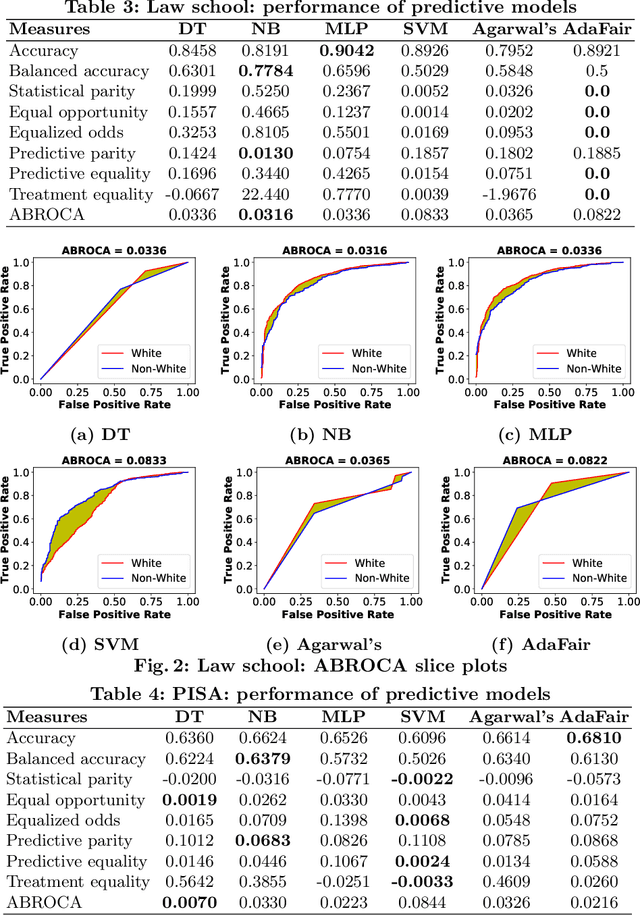
Predicting students' academic performance is one of the key tasks of educational data mining (EDM). Traditionally, the high forecasting quality of such models was deemed critical. More recently, the issues of fairness and discrimination w.r.t. protected attributes, such as gender or race, have gained attention. Although there are several fairness-aware learning approaches in EDM, a comparative evaluation of these measures is still missing. In this paper, we evaluate different group fairness measures for student performance prediction problems on various educational datasets and fairness-aware learning models. Our study shows that the choice of the fairness measure is important, likewise for the choice of the grade threshold.

Multiple Fairness and Cardinality constraints for Students-Topics Grouping Problem

Group work is a prevalent activity in educational settings, where students are often divided into topic-specific groups based on their preferences. The grouping should reflect the students' aspirations as much as possible. Usually, the resulting groups should also be balanced in terms of protected attributes like gender or race since studies indicate that students might learn better in a diverse group. Moreover, balancing the group cardinalities is also an essential requirement for fair workload distribution across the groups. In this paper, we introduce the multi-fair capacitated (MFC) grouping problem that fairly partitions students into non-overlapping groups while ensuring balanced group cardinalities (with a lower bound and an upper bound), and maximizing the diversity of members in terms of protected attributes. We propose two approaches: a heuristic method and a knapsack-based method to obtain the MFC grouping. The experiments on a real dataset and a semi-synthetic dataset show that our proposed methods can satisfy students' preferences well and deliver balanced and diverse groups regarding cardinality and the protected attribute, respectively.

Fair-Capacitated Clustering

Traditionally, clustering algorithms focus on partitioning the data into groups of similar instances. The similarity objective, however, is not sufficient in applications where a fair-representation of the groups in terms of protected attributes like gender or race, is required for each cluster. Moreover, in many applications, to make the clusters useful for the end-user, a balanced cardinality among the clusters is required. Our motivation comes from the education domain where studies indicate that students might learn better in diverse student groups and of course groups of similar cardinality are more practical e.g., for group assignments. To this end, we introduce the fair-capacitated clustering problem that partitions the data into clusters of similar instances while ensuring cluster fairness and balancing cluster cardinalities. We propose a two-step solution to the problem: i) we rely on fairlets to generate minimal sets that satisfy the fair constraint and ii) we propose two approaches, namely hierarchical clustering and partitioning-based clustering, to obtain the fair-capacitated clustering. The hierarchical approach embeds the additional cardinality requirements during the merging step while the partitioning-based one alters the assignment step using a knapsack problem formulation to satisfy the additional requirements. Our experiments on four educational datasets show that our approaches deliver well-balanced clusters in terms of both fairness and cardinality while maintaining a good clustering quality.