Steady-State Analysis and Online Learning for Queues with Hawkes Arrivals

We investigate the long-run behavior of single-server queues with Hawkes arrivals and general service distributions and related optimization problems. In detail, utilizing novel coupling techniques, we establish finite moment bounds for the stationary distribution of the workload and busy period processes. In addition, we are able to show that, those queueing processes converge exponentially fast to their stationary distribution. Based on these theoretic results, we develop an efficient numerical algorithm to solve the optimal staffing problem for the Hawkes queues in a data-driven manner. Numerical results indicate a sharp difference in staffing for Hawkes queues, compared to the classic GI/GI/1 model, especially in the heavy-traffic regime.

Online Learning and Optimization for Queues with Unknown Demand Curve and Service Distribution

We investigate an optimization problem in a queueing system where the service provider selects the optimal service fee p and service capacity \mu to maximize the cumulative expected profit (the service revenue minus the capacity cost and delay penalty). The conventional predict-then-optimize (PTO) approach takes two steps: first, it estimates the model parameters (e.g., arrival rate and service-time distribution) from data; second, it optimizes a model based on the estimated parameters. A major drawback of PTO is that its solution accuracy can often be highly sensitive to the parameter estimation errors because PTO is unable to properly link these errors (step 1) to the quality of the optimized solutions (step 2). To remedy this issue, we develop an online learning framework that automatically incorporates the aforementioned parameter estimation errors in the solution prescription process; it is an integrated method that can "learn" the optimal solution without needing to set up the parameter estimation as a separate step as in PTO. Effectiveness of our online learning approach is substantiated by (i) theoretical results including the algorithm convergence and analysis of the regret ("cost" to pay over time for the algorithm to learn the optimal policy), and (ii) engineering confirmation via simulation experiments of a variety of representative examples. We also provide careful comparisons for PTO and the online learning method.

An online learning approach to dynamic pricing and capacity sizing in service systems

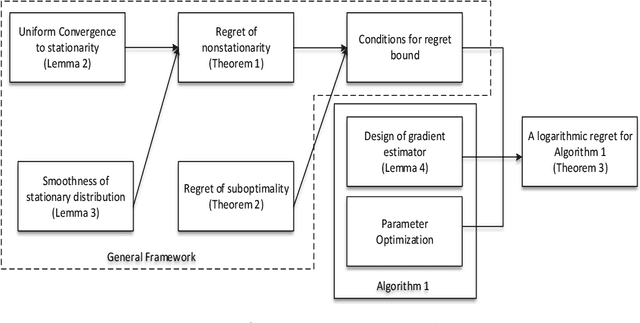
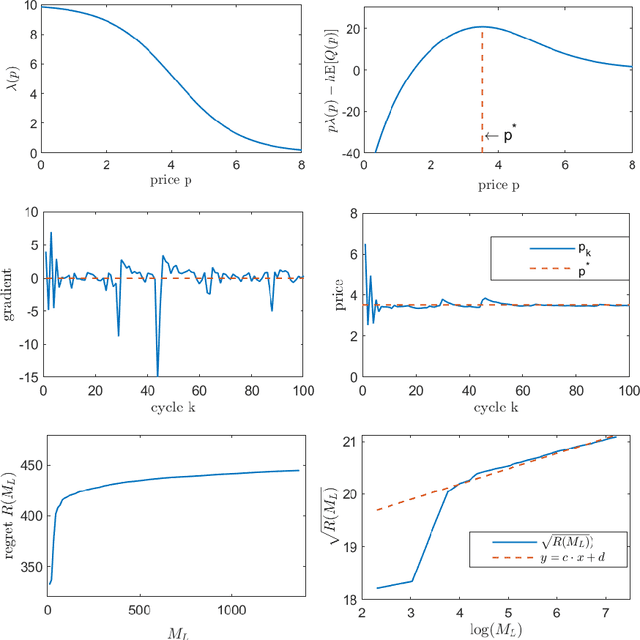
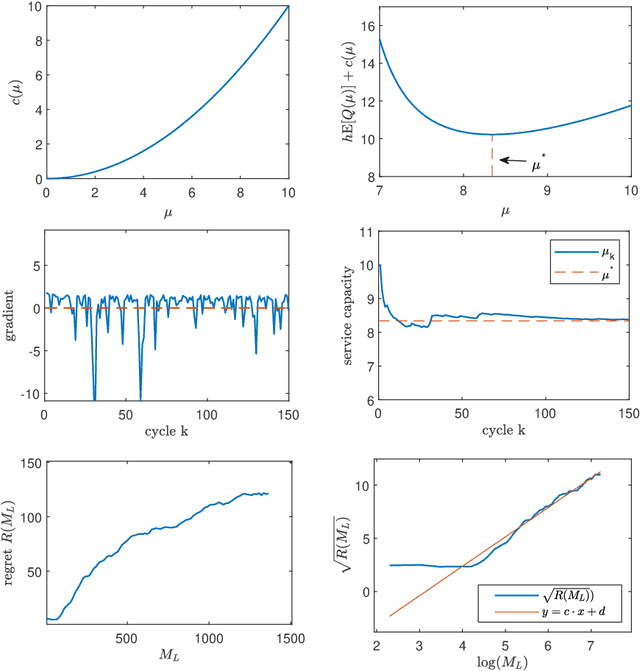
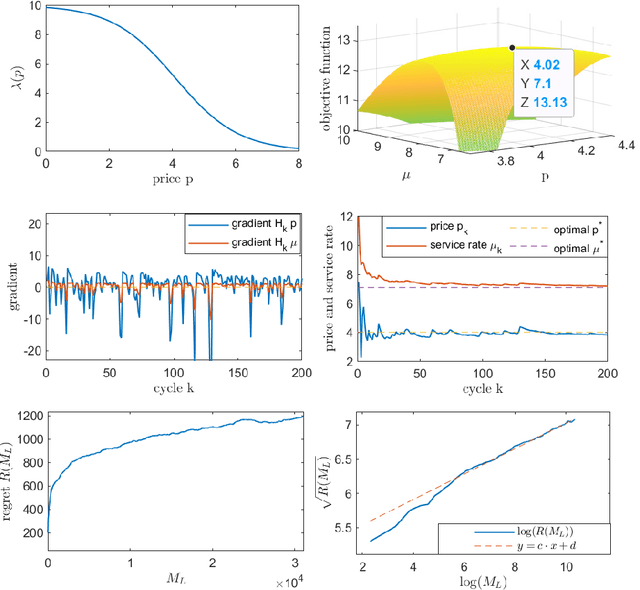
We study a dynamic pricing and capacity sizing problem in a GI/GI/1 queue, where the service provider's objective is to obtain the optimal service fee $p$ and service capacity $\mu$ so as to maximize cumulative expected profit (the service revenue minus the staffing cost and delay penalty). Due to the complex nature of the queueing dynamics, such a problem has no analytic solution so that previous research often resorts to heavy-traffic analysis in that both the arrival rate and service rate are sent to infinity. In this work we propose an online learning framework designed for solving this problem which does not require the system's scale to increase. Our algorithm organizes the time horizon into successive operational cycles and prescribes an efficient procedure to obtain improved pricing and staffing policies in each cycle using data collected in previous cycles. Data here include the number of customer arrivals, waiting times, and the server's busy times. The ingenuity of this approach lies in its online nature, which allows the service provider do better by interacting with the environment. Effectiveness of our online learning algorithm is substantiated by (i) theoretical results including the algorithm convergence and regret analysis (with a logarithmic regret bound), and (ii) engineering confirmation via simulation experiments of a variety of representative GI/GI/1 queues.