Guanqiang Zhou
Robust Distributed Learning Against Both Distributional Shifts and Byzantine Attacks
Oct 29, 2022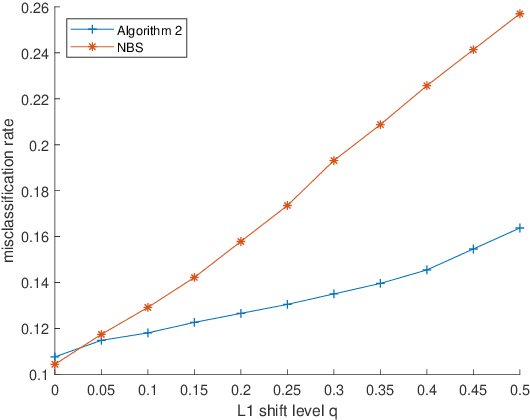
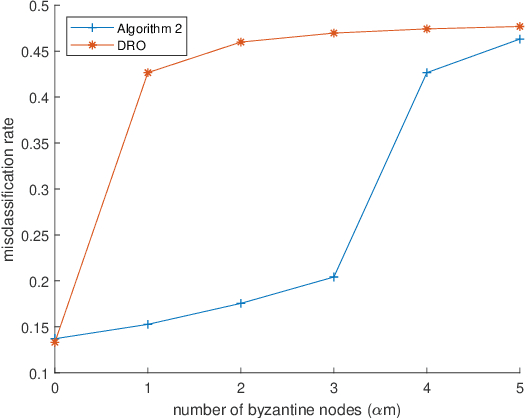
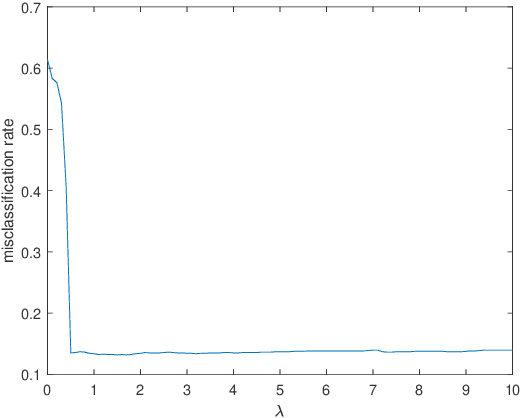
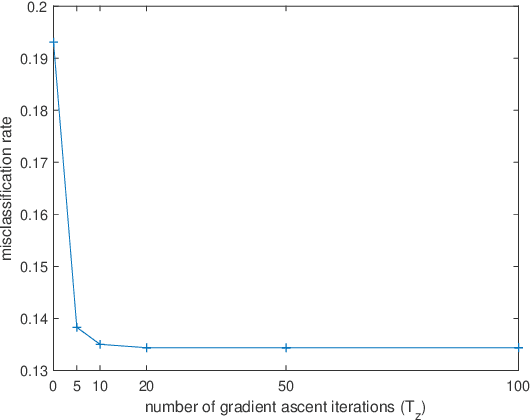
Abstract:In distributed learning systems, robustness issues may arise from two sources. On one hand, due to distributional shifts between training data and test data, the trained model could exhibit poor out-of-sample performance. On the other hand, a portion of working nodes might be subject to byzantine attacks which could invalidate the learning result. Existing works mostly deal with these two issues separately. In this paper, we propose a new algorithm that equips distributed learning with robustness measures against both distributional shifts and byzantine attacks. Our algorithm is built on recent advances in distributionally robust optimization as well as norm-based screening (NBS), a robust aggregation scheme against byzantine attacks. We provide convergence proofs in three cases of the learning model being nonconvex, convex, and strongly convex for the proposed algorithm, shedding light on its convergence behaviors and endurability against byzantine attacks. In particular, we deduce that any algorithm employing NBS (including ours) cannot converge when the percentage of byzantine nodes is 1/3 or higher, instead of 1/2, which is the common belief in current literature. The experimental results demonstrate the effectiveness of our algorithm against both robustness issues. To the best of our knowledge, this is the first work to address distributional shifts and byzantine attacks simultaneously.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge