Feasible strategies in three-way conflict analysis with three-valued ratings

Most existing work on three-way conflict analysis has focused on trisecting agent pairs, agents, or issues, which contributes to understanding the nature of conflicts but falls short in addressing their resolution. Specifically, the formulation of feasible strategies, as an essential component of conflict resolution and mitigation, has received insufficient scholarly attention. Therefore, this paper aims to investigate feasible strategies from two perspectives of consistency and non-consistency. Particularly, we begin with computing the overall rating of a clique of agents based on positive and negative similarity degrees. Afterwards, considering the weights of both agents and issues, we propose weighted consistency and non-consistency measures, which are respectively used to identify the feasible strategies for a clique of agents. Algorithms are developed to identify feasible strategies, $L$-order feasible strategies, and the corresponding optimal ones. Finally, to demonstrate the practicality, effectiveness, and superiority of the proposed models, we apply them to two commonly used case studies on NBA labor negotiations and development plans for Gansu Province and conduct a sensitivity analysis on parameters and a comparative analysis with existing state-of-the-art conflict analysis approaches. The comparison results demonstrate that our conflict resolution models outperform the conventional approaches by unifying weighted agent-issue evaluation with consistency and non-consistency measures to enable the systematic identification of not only feasible strategies but also optimal solutions.

Three-way conflict analysis based on alliance and conflict functions

Trisecting agents, issues, and agent pairs are essential topics of three-way conflict analysis. They have been commonly studied based on either a rating or an auxiliary function. A rating function defines the positive, negative, or neutral ratings of agents on issues. An auxiliary function defines the alliance, conflict, and neutrality relations between agents. These functions measure two opposite aspects in a single function, leading to challenges in interpreting their aggregations over a group of issues or agents. For example, when studying agent relations regarding a set of issues, a standard aggregation takes the average of an auxiliary function concerning single issues. Therefore, a pair of alliance +1 and conflict -1 relations will produce the same result as a pair of neutrality 0 relations, although the attitudes represented by the two pairs are very different. To clarify semantics, we separate the two opposite aspects in an auxiliary function into a pair of alliance and conflict functions. Accordingly, we trisect the agents, issues, and agent pairs and investigate their applications in solving a few crucial questions in conflict analysis. Particularly, we explore the concepts of alliance sets and strategies. A real-world application is given to illustrate the proposed models.

Granular-Balls based Fuzzy Twin Support Vector Machine for Classification

The twin support vector machine (TWSVM) classifier has attracted increasing attention because of its low computational complexity. However, its performance tends to degrade when samples are affected by noise. The granular-ball fuzzy support vector machine (GBFSVM) classifier partly alleviates the adverse effects of noise, but it relies solely on the distance between the granular-ball's center and the class center to design the granular-ball membership function. In this paper, we first introduce the granular-ball twin support vector machine (GBTWSVM) classifier, which integrates granular-ball computing (GBC) with the twin support vector machine (TWSVM) classifier. By replacing traditional point inputs with granular-balls, we demonstrate how to derive a pair of non-parallel hyperplanes for the GBTWSVM classifier by solving a quadratic programming problem. Subsequently, we design the membership and non-membership functions of granular-balls using Pythagorean fuzzy sets to differentiate the contributions of granular-balls in various regions. Additionally, we develop the granular-ball fuzzy twin support vector machine (GBFTSVM) classifier by incorporating GBC with the fuzzy twin support vector machine (FTSVM) classifier. We demonstrate how to derive a pair of non-parallel hyperplanes for the GBFTSVM classifier by solving a quadratic programming problem. We also design algorithms for the GBTSVM classifier and the GBFTSVM classifier. Finally, the superior classification performance of the GBTWSVM classifier and the GBFTSVM classifier on 20 benchmark datasets underscores their scalability, efficiency, and robustness in tackling classification tasks.

Three-Way Decisions-Based Conflict Analysis Models

Three-way decision theory, which trisects the universe with less risks or costs, is considered as a powerful mathematical tool for handling uncertainty in incomplete and imprecise information tables, and provides an effective tool for conflict analysis decision making in real-time situations. In this paper, we propose the concepts of the agreement, disagreement and neutral subsets of a strategy with two evaluation functions, which establish the three-way decisions-based conflict analysis models(TWDCAMs) for trisecting the universe of agents, and employ a pair of two-way decisions models to interpret the mechanism of the three-way decision rules for an agent. Subsequently, we develop the concepts of the agreement, disagreement and neutral strategies of an agent group with two evaluation functions, which build the TWDCAMs for trisecting the universe of issues, and take a couple of two-way decisions models to explain the mechanism of the three-way decision rules for an issue. Finally, we reconstruct Fan, Qi and Wei's conflict analysis models(FQWCAMs) and Sun, Ma and Zhao's conflict analysis models(SMZCAMs) with two evaluation functions, and interpret FQWCAMs and SMZCAMs with a pair of two-day decisions models, which illustrates that FQWCAMs and SMZCAMs are special cases of TWDCAMs.

Related family-based attribute reduction of covering information systems when varying attribute sets

In practical situations, there are many dynamic covering information systems with variations of attributes, but there are few studies on related family-based attribute reduction of dynamic covering information systems. In this paper, we first investigate updated mechanisms of constructing attribute reducts for consistent and inconsistent covering information systems when varying attribute sets by using related families. Then we employ examples to illustrate how to compute attribute reducts of dynamic covering information systems with variations of attribute sets. Finally, the experimental results illustrates that the related family-based methods are effective to perform attribute reduction of dynamic covering information systems when attribute sets are varying with time.

Conflict Analysis for Pythagorean Fuzzy Information Systems with Group Decision Making

Pythagorean fuzzy sets provide stronger ability than intuitionistic fuzzy sets to model uncertainty information and knowledge, but little effort has been paid to conflict analysis of Pythagorean fuzzy information systems. In this paper, we present three types of positive, central, and negative alliances with different thresholds, and employ examples to illustrate how to construct the positive, central, and negative alliances. Then we study conflict analysis of Pythagorean fuzzy information systems based on Bayesian minimum risk theory. Finally, we investigate group conflict analysis of Pythagorean fuzzy information systems based on Bayesian minimum risk theory.

Double-quantitative $γ^{\ast}-$fuzzy coverings approximation operators

In digital-based information boom, the fuzzy covering rough set model is an important mathematical tool for artificial intelligence, and how to build the bridge between the fuzzy covering rough set theory and Pawlak's model is becoming a hot research topic. In this paper, we first present the $\gamma-$fuzzy covering based probabilistic and grade approximation operators and double-quantitative approximation operators. We also study the relationships among the three types of $\gamma-$fuzzy covering based approximation operators. Second, we propose the $\gamma^{\ast}-$fuzzy coverings based multi-granulation probabilistic and grade lower and upper approximation operators and multi-granulation double-quantitative lower and upper approximation operators. We also investigate the relationships among these types of $\gamma-$fuzzy coverings based approximation operators. Finally, we employ several examples to illustrate how to construct the lower and upper approximations of fuzzy sets with the absolute and relative quantitative information.

Knowledge reduction of dynamic covering decision information systems with immigration of more objects

In practical situations, it is of interest to investigate computing approximations of sets as an important step of knowledge reduction of dynamic covering decision information systems. In this paper, we present incremental approaches to computing the type-1 and type-2 characteristic matrices of dynamic coverings whose cardinalities increase with immigration of more objects. We also present the incremental algorithms of computing the second and sixth lower and upper approximations of sets in dynamic covering approximation spaces.

Decision-theoretic rough sets-based three-way approximations of interval-valued fuzzy sets

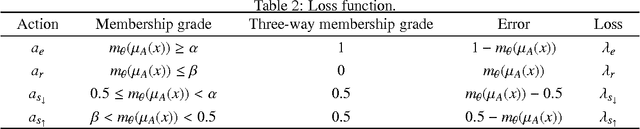
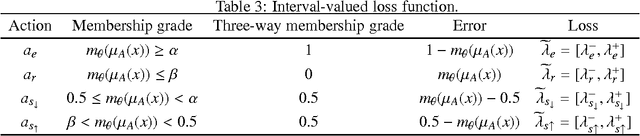
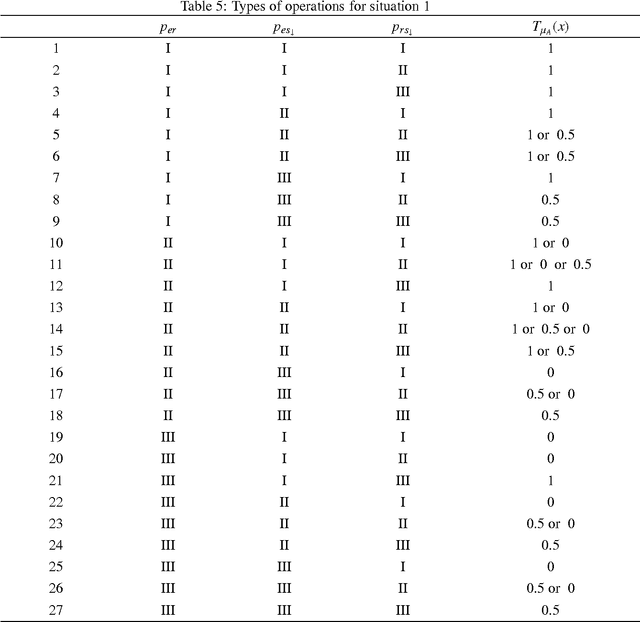
In practical situations, interval-valued fuzzy sets are frequently encountered. In this paper, firstly, we present shadowed sets for interpreting and understanding interval fuzzy sets. We also provide an analytic solution to computing the pair of thresholds by searching for a balance of uncertainty in the framework of shadowed sets. Secondly, we construct errors-based three-way approximations of interval-valued fuzzy sets. We also provide an alternative decision-theoretic formulation for calculating the pair of thresholds by transforming interval-valued loss functions into single-valued loss functions, in which the required thresholds are computed by minimizing decision costs. Thirdly, we compute errors-based three-way approximations of interval-valued fuzzy sets by using interval-valued loss functions. Finally, we employ several examples to illustrate that how to take an action for an object with interval-valued membership grade by using interval-valued loss functions.