Decision-theoretic rough sets-based three-way approximations of interval-valued fuzzy sets
Paper and Code
Dec 22, 2014
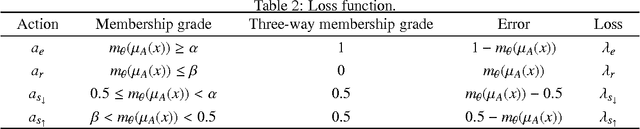
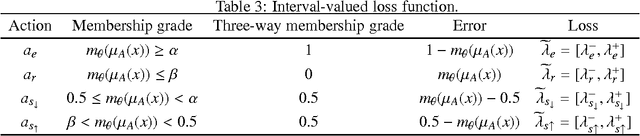
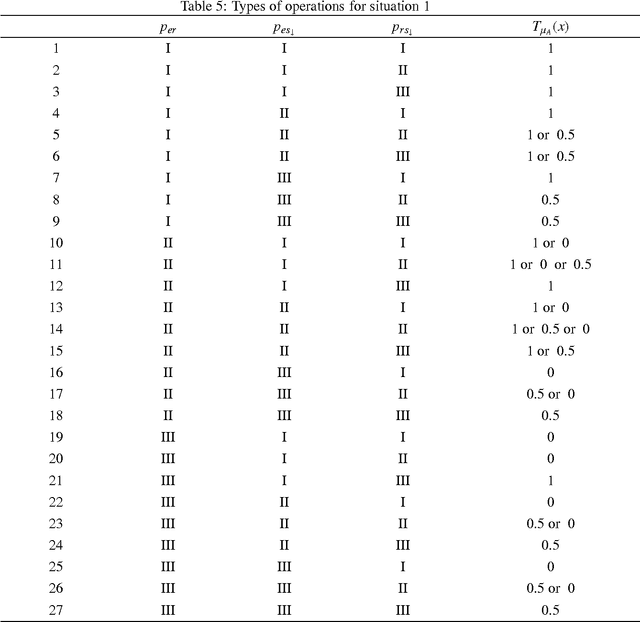
In practical situations, interval-valued fuzzy sets are frequently encountered. In this paper, firstly, we present shadowed sets for interpreting and understanding interval fuzzy sets. We also provide an analytic solution to computing the pair of thresholds by searching for a balance of uncertainty in the framework of shadowed sets. Secondly, we construct errors-based three-way approximations of interval-valued fuzzy sets. We also provide an alternative decision-theoretic formulation for calculating the pair of thresholds by transforming interval-valued loss functions into single-valued loss functions, in which the required thresholds are computed by minimizing decision costs. Thirdly, we compute errors-based three-way approximations of interval-valued fuzzy sets by using interval-valued loss functions. Finally, we employ several examples to illustrate that how to take an action for an object with interval-valued membership grade by using interval-valued loss functions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge