ElementaryNet: A Non-Strategic Neural Network for Predicting Human Behavior in Normal-Form Games

Models of human behavior in game-theoretic settings often distinguish between strategic behavior, in which a player both reasons about how others will act and best responds to these beliefs, and "level-0" non-strategic behavior, in which they do not respond to explicit beliefs about others. The state of the art for predicting human behavior on unrepeated simultaneous-move games is GameNet, a neural network that learns extremely complex level-0 specifications from data. The current paper makes three contributions. First, it shows that GameNet's level-0 specifications are too powerful, because they are capable of strategic reasoning. Second, it introduces a novel neural network architecture (dubbed ElementaryNet) and proves that it is only capable of nonstrategic behavior. Third, it describes an extensive experimental evaluation of ElementaryNet. Our overall findings are that (1) ElementaryNet dramatically underperforms GameNet when neither model is allowed to explicitly model higher level agents who best-respond to the model's predictions, indicating that good performance on our dataset requires a model capable of strategic reasoning; (2) that the two models achieve statistically indistinguishable performance when such higher-level agents are introduced, meaning that ElementaryNet's restriction to a non-strategic level-0 specification does not degrade model performance; and (3) that this continues to hold even when ElementaryNet is restricted to a set of level-0 building blocks previously introduced in the literature, with only the functional form being learned by the neural network.

Understanding Iterative Combinatorial Auction Designs via Multi-Agent Reinforcement Learning

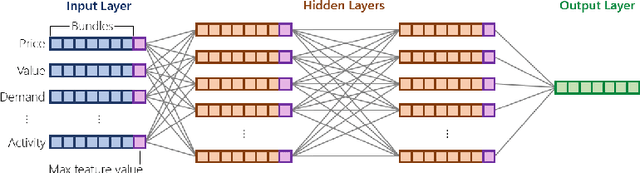
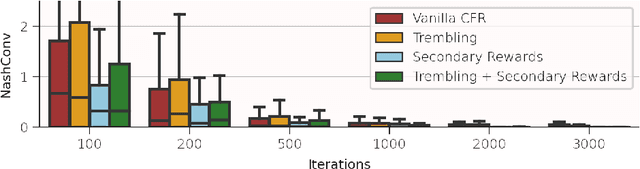
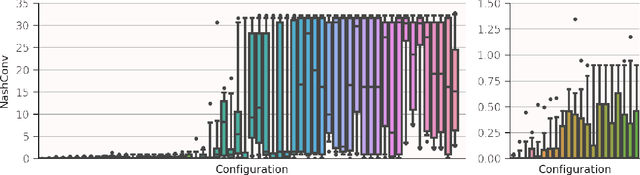
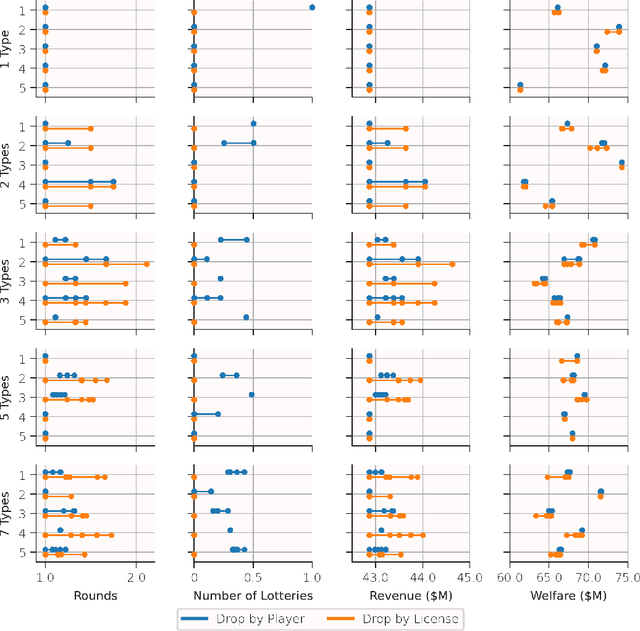
Iterative combinatorial auctions are widely used in high stakes settings such as spectrum auctions. Such auctions can be hard to understand analytically, making it difficult for bidders to determine how to behave and for designers to optimize auction rules to ensure desirable outcomes such as high revenue or welfare. In this paper, we investigate whether multi-agent reinforcement learning (MARL) algorithms can be used to understand iterative combinatorial auctions, given that these algorithms have recently shown empirical success in several other domains. We find that MARL can indeed benefit auction analysis, but that deploying it effectively is nontrivial. We begin by describing modelling decisions that keep the resulting game tractable without sacrificing important features such as imperfect information or asymmetry between bidders. We also discuss how to navigate pitfalls of various MARL algorithms, how to overcome challenges in verifying convergence, and how to generate and interpret multiple equilibria. We illustrate the promise of our resulting approach by using it to evaluate a specific rule change to a clock auction, finding substantially different auction outcomes due to complex changes in bidders' behavior.

Loss Functions for Behavioral Game Theory

Behavioral game theorists all use experimental data to evaluate predictive models of human behavior. However, they differ greatly in their choice of loss function for these evaluations, with error rate, negative log-likelihood, cross-entropy, Brier score, and L2 error all being common choices. We attempt to offer a principled answer to the question of which loss functions make sense for this task, formalizing desiderata that we argue loss functions should satisfy. We construct a family of loss functions, which we dub "diagonal bounded Bregman divergences", that satisfy all of these axioms and includes the squared L2 error. In fact, the squared L2 error is the only acceptable loss that is relatively commonly used in practice; we thus recommend its continued use to behavioral game theorists.

Better Peer Grading through Bayesian Inference

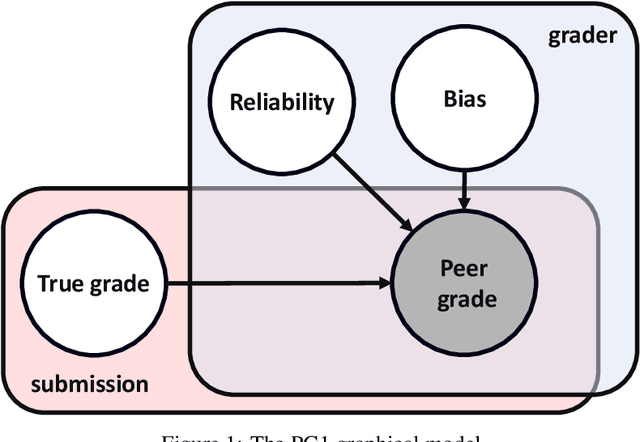
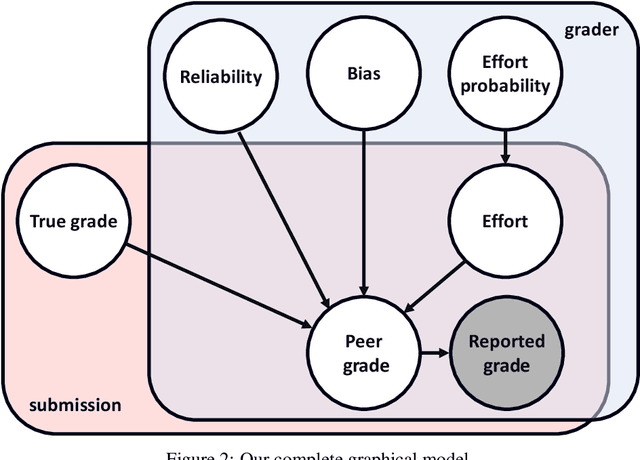
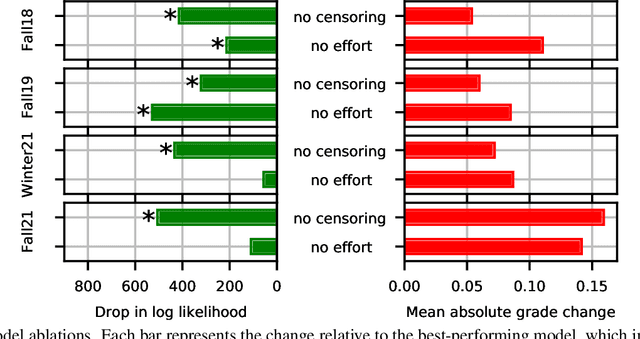
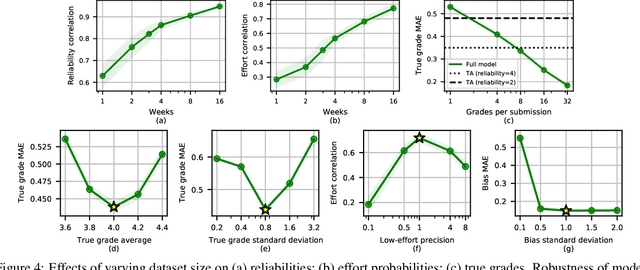
Peer grading systems aggregate noisy reports from multiple students to approximate a true grade as closely as possible. Most current systems either take the mean or median of reported grades; others aim to estimate students' grading accuracy under a probabilistic model. This paper extends the state of the art in the latter approach in three key ways: (1) recognizing that students can behave strategically (e.g., reporting grades close to the class average without doing the work); (2) appropriately handling censored data that arises from discrete-valued grading rubrics; and (3) using mixed integer programming to improve the interpretability of the grades assigned to students. We show how to make Bayesian inference practical in this model and evaluate our approach on both synthetic and real-world data obtained by using our implemented system in four large classes. These extensive experiments show that grade aggregation using our model accurately estimates true grades, students' likelihood of submitting uninformative grades, and the variation in their inherent grading error; we also characterize our models' robustness.

The Spotlight: A General Method for Discovering Systematic Errors in Deep Learning Models

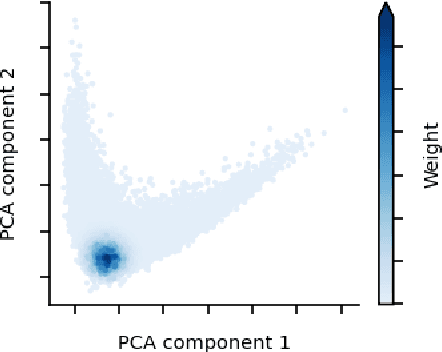
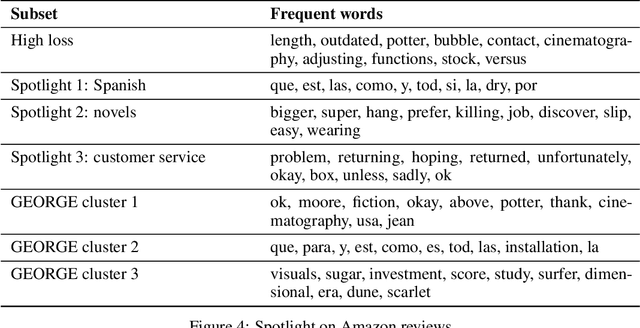
Supervised learning models often make systematic errors on rare subsets of the data. However, such systematic errors can be difficult to identify, as model performance can only be broken down across sensitive groups when these groups are known and explicitly labelled. This paper introduces a method for discovering systematic errors, which we call the spotlight. The key idea is that similar inputs tend to have similar representations in the final hidden layer of a neural network. We leverage this structure by "shining a spotlight" on this representation space to find contiguous regions where the model performs poorly. We show that the spotlight surfaces semantically meaningful areas of weakness in a wide variety of model architectures, including image classifiers, language models, and recommender systems.