Optimization of a Hydrodynamic Computational Reservoir through Evolution

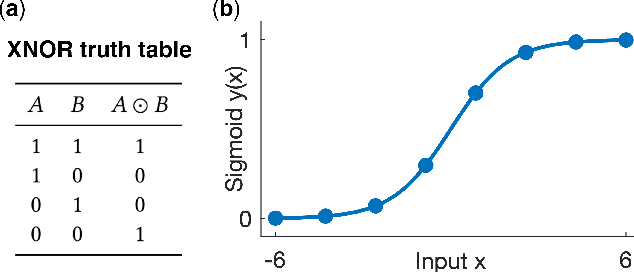
As demand for computational resources reaches unprecedented levels, research is expanding into the use of complex material substrates for computing. In this study, we interface with a model of a hydrodynamic system, under development by a startup, as a computational reservoir and optimize its properties using an evolution in materio approach. Input data are encoded as waves applied to our shallow water reservoir, and the readout wave height is obtained at a fixed detection point. We optimized the readout times and how inputs are mapped to the wave amplitude or frequency using an evolutionary search algorithm, with the objective of maximizing the system's ability to linearly separate observations in the training data by maximizing the readout matrix determinant. Applying evolutionary methods to this reservoir system substantially improved separability on an XNOR task, in comparison to implementations with hand-selected parameters. We also applied our approach to a regression task and show that our approach improves out-of-sample accuracy. Results from this study will inform how we interface with the physical reservoir in future work, and we will use these methods to continue to optimize other aspects of the physical implementation of this system as a computational reservoir.

Theory of neuromorphic computing by waves: machine learning by rogue waves, dispersive shocks, and solitons

We study artificial neural networks with nonlinear waves as a computing reservoir. We discuss universality and the conditions to learn a dataset in terms of output channels and nonlinearity. A feed-forward three-layer model, with an encoding input layer, a wave layer, and a decoding readout, behaves as a conventional neural network in approximating mathematical functions, real-world datasets, and universal Boolean gates. The rank of the transmission matrix has a fundamental role in assessing the learning abilities of the wave. For a given set of training points, a threshold nonlinearity for universal interpolation exists. When considering the nonlinear Schroedinger equation, the use of highly nonlinear regimes implies that solitons, rogue, and shock waves do have a leading role in training and computing. Our results may enable the realization of novel machine learning devices by using diverse physical systems, as nonlinear optics, hydrodynamics, polaritonics, and Bose-Einstein condensates. The application of these concepts to photonics opens the way to a large class of accelerators and new computational paradigms. In complex wave systems, as multimodal fibers, integrated optical circuits, random, topological devices, and metasurfaces, nonlinear waves can be employed to perform computation and solve complex combinatorial optimization.

Programming multi-level quantum gates in disordered computing reservoirs via machine learning

Novel computational tools in machine learning open new perspectives in quantum information systems. Here we adopt the open-source programming library Tensorflow to design multi-level quantum gates including a computing reservoir represented by a random unitary matrix. In optics, the reservoir is a disordered medium or a multimodal fiber. We show that by using trainable operators at the input and at the readout, it is possible to realize multi-level gates. We study single and qudit gates, including the scaling properties of the algorithms with the size of the reservoir.