Efficient Computation Using Spatial-Photonic Ising Machines: Utilizing Low-Rank and Circulant Matrix Constraints

We explore the potential of spatial-photonic Ising machines (SPIMs) to address computationally intensive Ising problems that employ low-rank and circulant coupling matrices. Our results indicate that the performance of SPIMs is critically affected by the rank and precision of the coupling matrices. By developing and assessing advanced decomposition techniques, we expand the range of problems SPIMs can solve, overcoming the limitations of traditional Mattis-type matrices. Our approach accommodates a diverse array of coupling matrices, including those with inherently low ranks, applicable to complex NP-complete problems. We explore the practical benefits of low-rank approximation in optimization tasks, particularly in financial optimization, to demonstrate the real-world applications of SPIMs. Finally, we evaluate the computational limitations imposed by SPIM hardware precision and suggest strategies to optimize the performance of these systems within these constraints.

Boson sampling discrete solitons by quantum machine learning

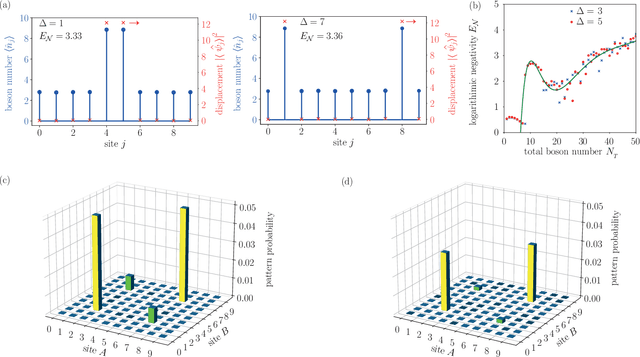
We use a neural network variational ansatz to compute Gaussian quantum discrete solitons in an array of waveguides described by the quantum discrete nonlinear Schroedinger equation. By training the quantum machine learning model in the phase space, we find different quantum soliton solutions varying the number of particles and interaction strength. The use of Gaussian states enables measuring the degree of entanglement and the boson sampling patterns. We compute the probability of generating different particle pairs when varying the soliton features and unveil that bound states of discrete solitons emit correlated pairs of photons. These results may have a role in boson sampling experiments with nonlinear systems and in developing quantum processors to generate entangled many-photon nonlinear states.

Gaussian boson sampling and multi-particle event optimization by machine learning in the quantum phase space

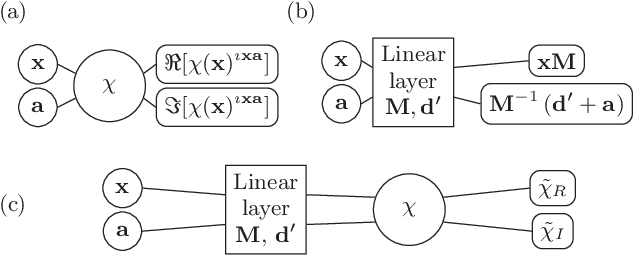
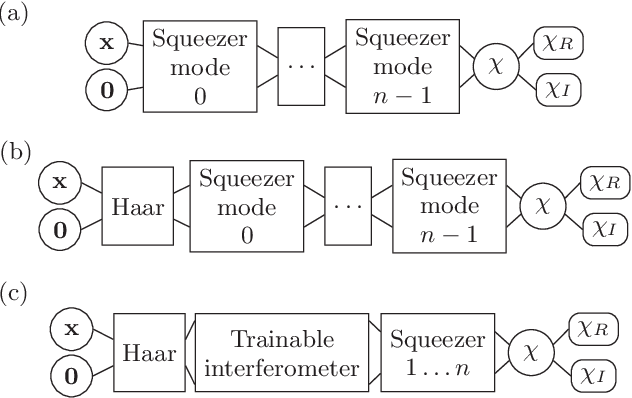
We use neural networks to represent the characteristic function of many-body Gaussian states in the quantum phase space. By a pullback mechanism, we model transformations due to unitary operators as linear layers that can be cascaded to simulate complex multi-particle processes. We use the layered neural networks for non-classical light propagation in random interferometers, and compute boson pattern probabilities by automatic differentiation. We also demonstrate that multi-particle events in Gaussian boson sampling can be optimized by a proper design and training of the neural network weights. The results are potentially useful to the creation of new sources and complex circuits for quantum technologies.

Theory of neuromorphic computing by waves: machine learning by rogue waves, dispersive shocks, and solitons

We study artificial neural networks with nonlinear waves as a computing reservoir. We discuss universality and the conditions to learn a dataset in terms of output channels and nonlinearity. A feed-forward three-layer model, with an encoding input layer, a wave layer, and a decoding readout, behaves as a conventional neural network in approximating mathematical functions, real-world datasets, and universal Boolean gates. The rank of the transmission matrix has a fundamental role in assessing the learning abilities of the wave. For a given set of training points, a threshold nonlinearity for universal interpolation exists. When considering the nonlinear Schroedinger equation, the use of highly nonlinear regimes implies that solitons, rogue, and shock waves do have a leading role in training and computing. Our results may enable the realization of novel machine learning devices by using diverse physical systems, as nonlinear optics, hydrodynamics, polaritonics, and Bose-Einstein condensates. The application of these concepts to photonics opens the way to a large class of accelerators and new computational paradigms. In complex wave systems, as multimodal fibers, integrated optical circuits, random, topological devices, and metasurfaces, nonlinear waves can be employed to perform computation and solve complex combinatorial optimization.

Programming multi-level quantum gates in disordered computing reservoirs via machine learning

Novel computational tools in machine learning open new perspectives in quantum information systems. Here we adopt the open-source programming library Tensorflow to design multi-level quantum gates including a computing reservoir represented by a random unitary matrix. In optics, the reservoir is a disordered medium or a multimodal fiber. We show that by using trainable operators at the input and at the readout, it is possible to realize multi-level gates. We study single and qudit gates, including the scaling properties of the algorithms with the size of the reservoir.