Asymptotic analysis of shallow and deep forgetting in replay with Neural Collapse

A persistent paradox in continual learning (CL) is that neural networks often retain linearly separable representations of past tasks even when their output predictions fail. We formalize this distinction as the gap between deep feature-space and shallow classifier-level forgetting. We reveal a critical asymmetry in Experience Replay: while minimal buffers successfully anchor feature geometry and prevent deep forgetting, mitigating shallow forgetting typically requires substantially larger buffer capacities. To explain this, we extend the Neural Collapse framework to the sequential setting. We characterize deep forgetting as a geometric drift toward out-of-distribution subspaces and prove that any non-zero replay fraction asymptotically guarantees the retention of linear separability. Conversely, we identify that the "strong collapse" induced by small buffers leads to rank-deficient covariances and inflated class means, effectively blinding the classifier to true population boundaries. By unifying CL with out-of-distribution detection, our work challenges the prevailing reliance on large buffers, suggesting that explicitly correcting these statistical artifacts could unlock robust performance with minimal replay.

Local vs Global continual learning

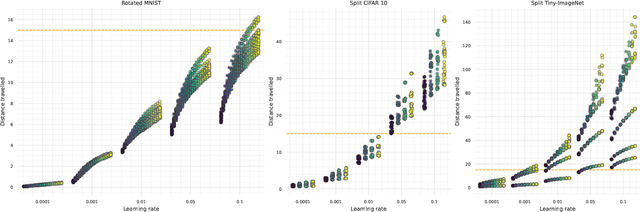
Continual learning is the problem of integrating new information in a model while retaining the knowledge acquired in the past. Despite the tangible improvements achieved in recent years, the problem of continual learning is still an open one. A better understanding of the mechanisms behind the successes and failures of existing continual learning algorithms can unlock the development of new successful strategies. In this work, we view continual learning from the perspective of the multi-task loss approximation, and we compare two alternative strategies, namely local and global approximations. We classify existing continual learning algorithms based on the approximation used, and we assess the practical effects of this distinction in common continual learning settings.Additionally, we study optimal continual learning objectives in the case of local polynomial approximations and we provide examples of existing algorithms implementing the optimal objectives

Towards guarantees for parameter isolation in continual learning

Deep learning has proved to be a successful paradigm for solving many challenges in machine learning. However, deep neural networks fail when trained sequentially on multiple tasks, a shortcoming known as catastrophic forgetting in the continual learning literature. Despite a recent flourish of learning algorithms successfully addressing this problem, we find that provable guarantees against catastrophic forgetting are lacking. In this work, we study the relationship between learning and forgetting by looking at the geometry of neural networks' loss landscape. We offer a unifying perspective on a family of continual learning algorithms, namely methods based on parameter isolation, and we establish guarantees on catastrophic forgetting for some of them.