Applying Lie Groups Approaches for Rigid Registration of Point Clouds

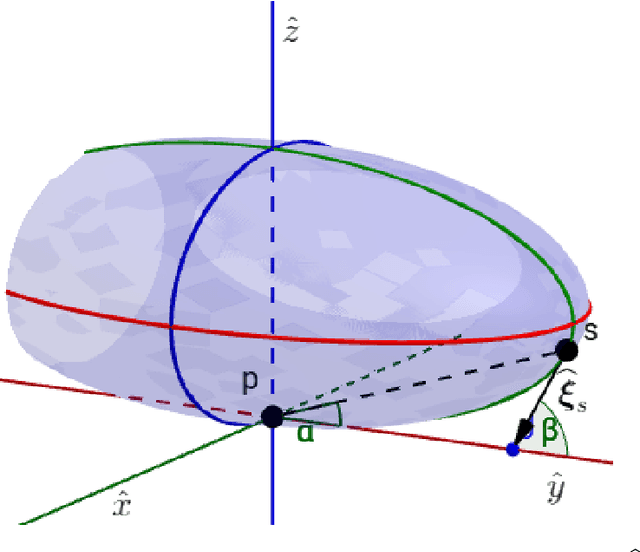
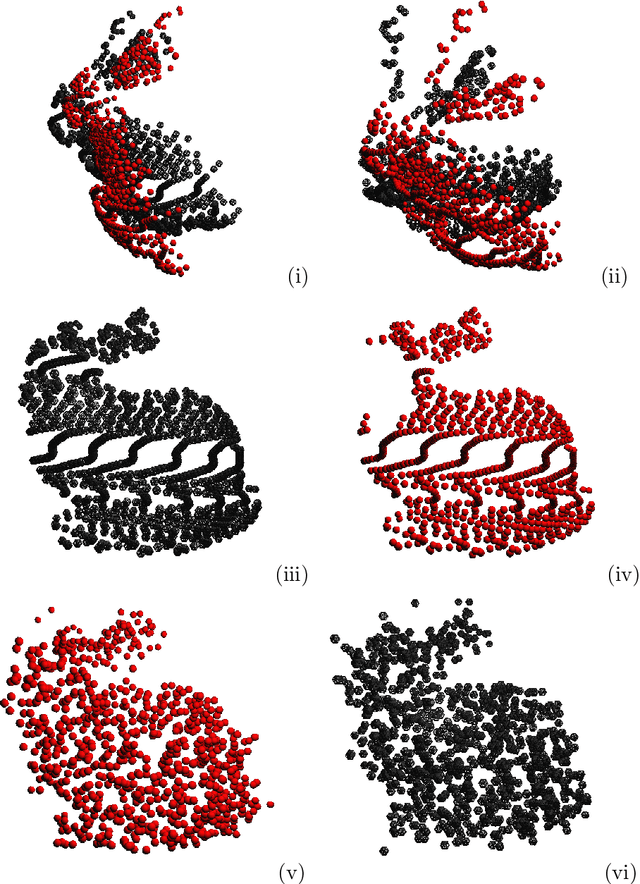
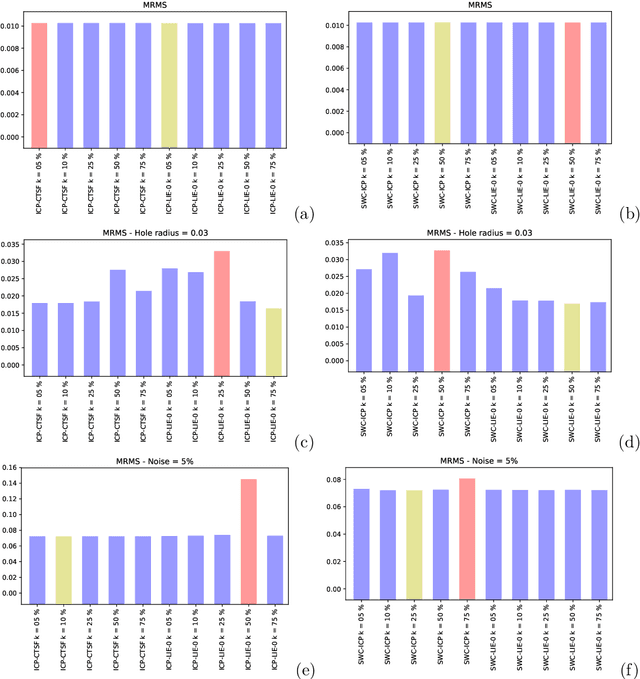
In the last decades, some literature appeared using the Lie groups theory to solve problems in computer vision. On the other hand, Lie algebraic representations of the transformations therein were introduced to overcome the difficulties behind group structure by mapping the transformation groups to linear spaces. In this paper we focus on application of Lie groups and Lie algebras to find the rigid transformation that best register two surfaces represented by point clouds. The so called pairwise rigid registration can be formulated by comparing intrinsic second-order orientation tensors that encode local geometry. These tensors can be (locally) represented by symmetric non-negative definite matrices. In this paper we interpret the obtained tensor field as a multivariate normal model. So, we start with the fact that the space of Gaussians can be equipped with a Lie group structure, that is isomorphic to a subgroup of the upper triangular matrices. Consequently, the associated Lie algebra structure enables us to handle Gaussians, and consequently, to compare orientation tensors, with Euclidean operations. We apply this methodology to variants of the Iterative Closest Point (ICP), a known technique for pairwise registration. We compare the obtained results with the original implementations that apply the comparative tensor shape factor (CTSF), which is a similarity notion based on the eigenvalues of the orientation tensors. We notice that the similarity measure in tensor spaces directly derived from Lie's approach is not invariant under rotations, which is a problem in terms of rigid registration. Despite of this, the performed computational experiments show promising results when embedding orientation tensor fields in Lie algebras.

Is human face processing a feature- or pattern-based task? Evidence using a unified computational method driven by eye movements

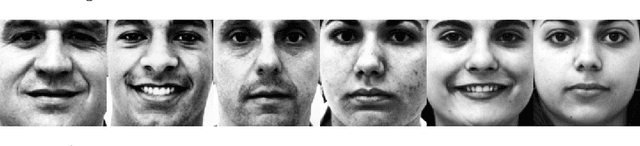
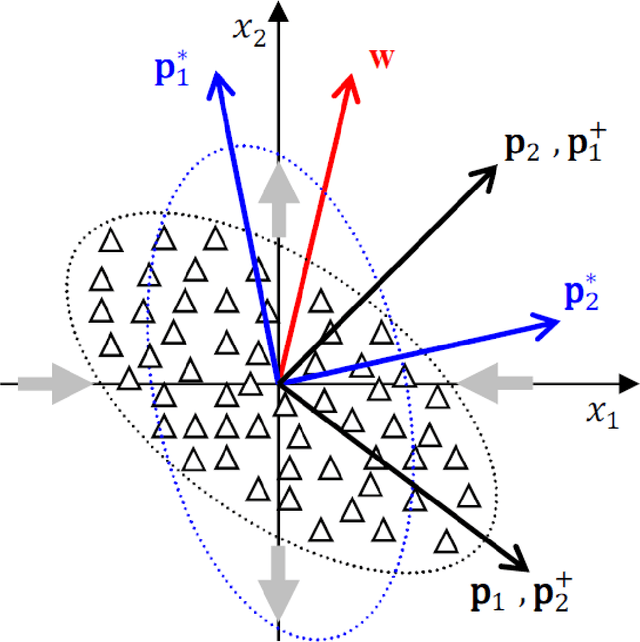
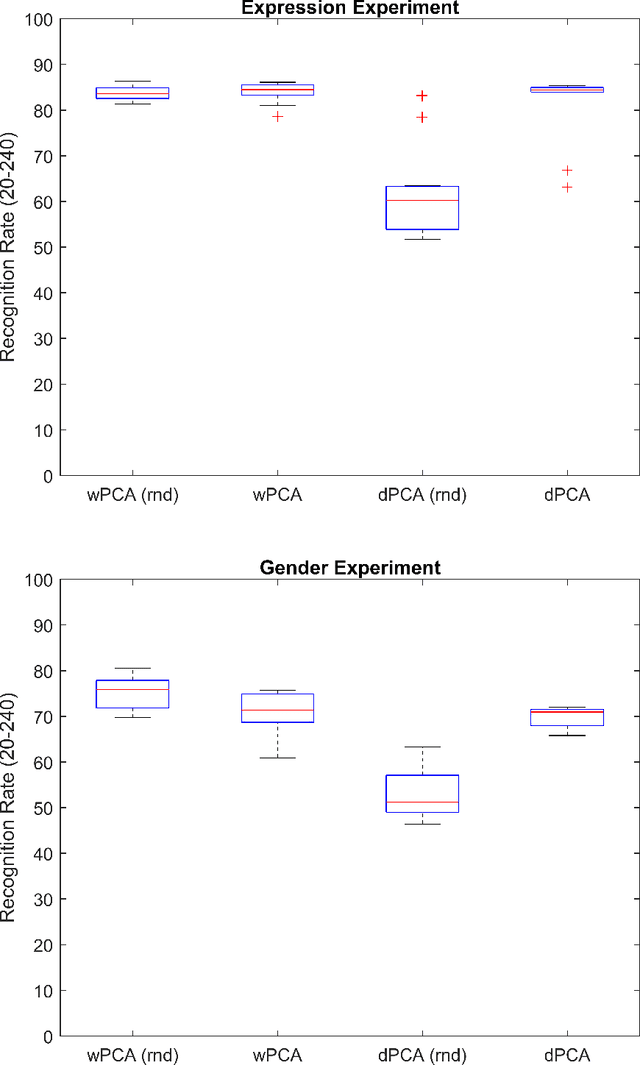
Research on human face processing using eye movements has provided evidence that we recognize face images successfully focusing our visual attention on a few inner facial regions, mainly on the eyes, nose and mouth. To understand how we accomplish this process of coding high-dimensional faces so efficiently, this paper proposes and implements a multivariate extraction method that combines face images variance with human spatial attention maps modeled as feature- and pattern-based information sources. It is based on a unified multidimensional representation of the well-known face-space concept. The spatial attention maps are summary statistics of the eye-tracking fixations of a number of participants and trials to frontal and well-framed face images during separate gender and facial expression recognition tasks. Our experimental results carried out on publicly available face databases have indicated that we might emulate the human extraction system as a pattern-based computational method rather than a feature-based one to properly explain the proficiency of the human system in recognizing visual face information.

Gradient Vector Flow Models for Boundary Extraction in 2D Images

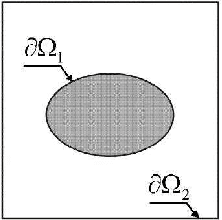
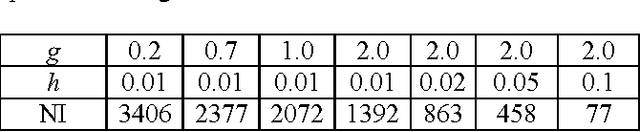
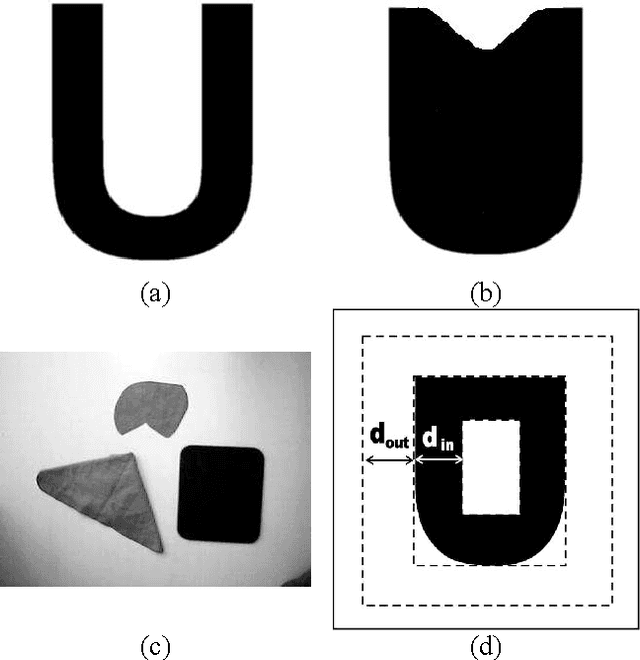
The Gradient Vector Flow (GVF) is a vector diffusion approach based on Partial Differential Equations (PDEs). This method has been applied together with snake models for boundary extraction medical images segmentation. The key idea is to use a diffusion-reaction PDE to generate a new external force field that makes snake models less sensitivity to initialization as well as improves the snake's ability to move into boundary concavities. In this paper, we firstly review basic results about convergence and numerical analysis of usual GVF schemes. We point out that GVF presents numerical problems due to discontinuities image intensity. This point is considered from a practical viewpoint from which the GVF parameters must follow a relationship in order to improve numerical convergence. Besides, we present an analytical analysis of the GVF dependency from the parameters values. Also, we observe that the method can be used for multiply connected domains by just imposing the suitable boundary condition. In the experimental results we verify these theoretical points and demonstrate the utility of GVF on a segmentation approach that we have developed based on snakes.

Genetic Algorithms and Quantum Computation

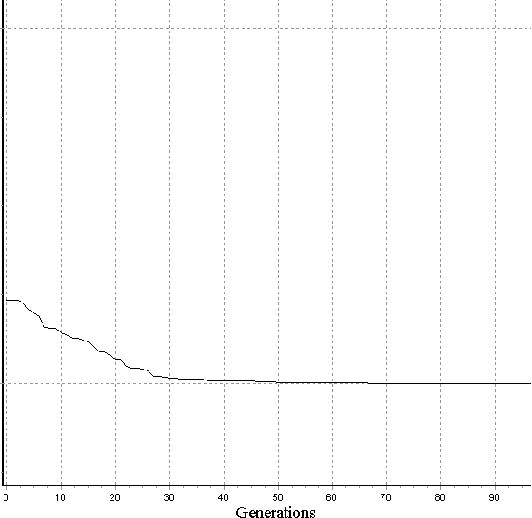
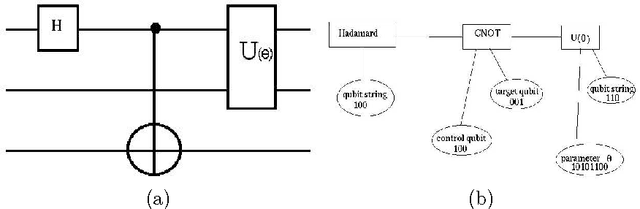
Recently, researchers have applied genetic algorithms (GAs) to address some problems in quantum computation. Also, there has been some works in the designing of genetic algorithms based on quantum theoretical concepts and techniques. The so called Quantum Evolutionary Programming has two major sub-areas: Quantum Inspired Genetic Algorithms (QIGAs) and Quantum Genetic Algorithms (QGAs). The former adopts qubit chromosomes as representations and employs quantum gates for the search of the best solution. The later tries to solve a key question in this field: what GAs will look like as an implementation on quantum hardware? As we shall see, there is not a complete answer for this question. An important point for QGAs is to build a quantum algorithm that takes advantage of both the GA and quantum computing parallelism as well as true randomness provided by quantum computers. In the first part of this paper we present a survey of the main works in GAs plus quantum computing including also our works in this area. Henceforth, we review some basic concepts in quantum computation and GAs and emphasize their inherent parallelism. Next, we review the application of GAs for learning quantum operators and circuit design. Then, quantum evolutionary programming is considered. Finally, we present our current research in this field and some perspectives.