Applying Lie Groups Approaches for Rigid Registration of Point Clouds

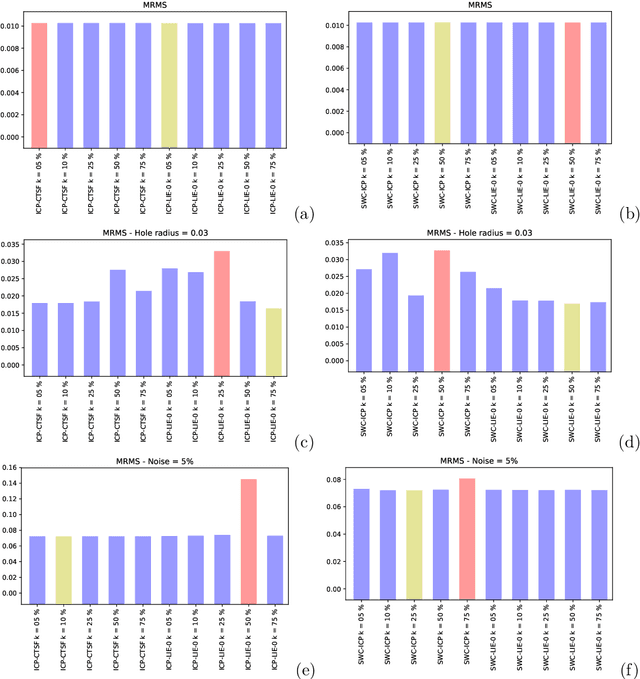
In the last decades, some literature appeared using the Lie groups theory to solve problems in computer vision. On the other hand, Lie algebraic representations of the transformations therein were introduced to overcome the difficulties behind group structure by mapping the transformation groups to linear spaces. In this paper we focus on application of Lie groups and Lie algebras to find the rigid transformation that best register two surfaces represented by point clouds. The so called pairwise rigid registration can be formulated by comparing intrinsic second-order orientation tensors that encode local geometry. These tensors can be (locally) represented by symmetric non-negative definite matrices. In this paper we interpret the obtained tensor field as a multivariate normal model. So, we start with the fact that the space of Gaussians can be equipped with a Lie group structure, that is isomorphic to a subgroup of the upper triangular matrices. Consequently, the associated Lie algebra structure enables us to handle Gaussians, and consequently, to compare orientation tensors, with Euclidean operations. We apply this methodology to variants of the Iterative Closest Point (ICP), a known technique for pairwise registration. We compare the obtained results with the original implementations that apply the comparative tensor shape factor (CTSF), which is a similarity notion based on the eigenvalues of the orientation tensors. We notice that the similarity measure in tensor spaces directly derived from Lie's approach is not invariant under rotations, which is a problem in terms of rigid registration. Despite of this, the performed computational experiments show promising results when embedding orientation tensor fields in Lie algebras.