Single-Qudit Quantum Neural Networks for Multiclass Classification

This paper proposes a single-qudit quantum neural network for multiclass classification, by using the enhanced representational capacity of high-dimensional qudit states. Our design employs an $d$-dimensional unitary operator, where $d$ corresponds to the number of classes, constructed using the Cayley transform of a skew-symmetric matrix, to efficiently encode and process class information. This architecture enables a direct mapping between class labels and quantum measurement outcomes, reducing circuit depth and computational overhead. To optimize network parameters, we introduce a hybrid training approach that combines an extended activation function -- derived from a truncated multivariable Taylor series expansion -- with support vector machine optimization for weight determination. We evaluate our model on the MNIST and EMNIST datasets, demonstrating competitive accuracy while maintaining a compact single-qudit quantum circuit. Our findings highlight the potential of qudit-based QNNs as scalable alternatives to classical deep learning models, particularly for multiclass classification. However, practical implementation remains constrained by current quantum hardware limitations. This research advances quantum machine learning by demonstrating the feasibility of higher-dimensional quantum systems for efficient learning tasks.

Regression and Classification with Single-Qubit Quantum Neural Networks

Since classical machine learning has become a powerful tool for developing data-driven algorithms, quantum machine learning is expected to similarly impact the development of quantum algorithms. The literature reflects a mutually beneficial relationship between machine learning and quantum computing, where progress in one field frequently drives improvements in the other. Motivated by the fertile connection between machine learning and quantum computing enabled by parameterized quantum circuits, we use a resource-efficient and scalable Single-Qubit Quantum Neural Network (SQQNN) for both regression and classification tasks. The SQQNN leverages parameterized single-qubit unitary operators and quantum measurements to achieve efficient learning. To train the model, we use gradient descent for regression tasks. For classification, we introduce a novel training method inspired by the Taylor series, which can efficiently find a global minimum in a single step. This approach significantly accelerates training compared to iterative methods. Evaluated across various applications, the SQQNN exhibits virtually error-free and strong performance in regression and classification tasks, including the MNIST dataset. These results demonstrate the versatility, scalability, and suitability of the SQQNN for deployment on near-term quantum devices.

Genetic Algorithms and Quantum Computation

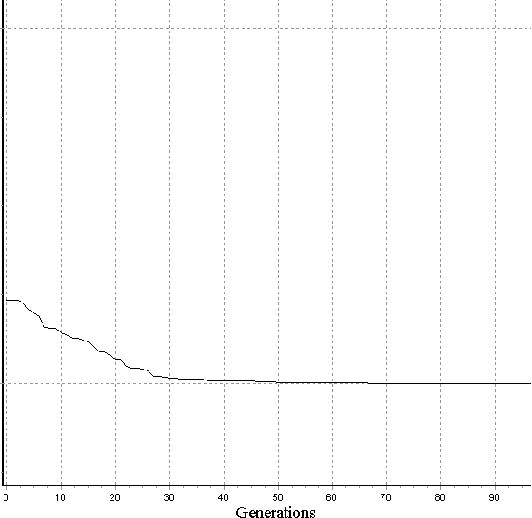
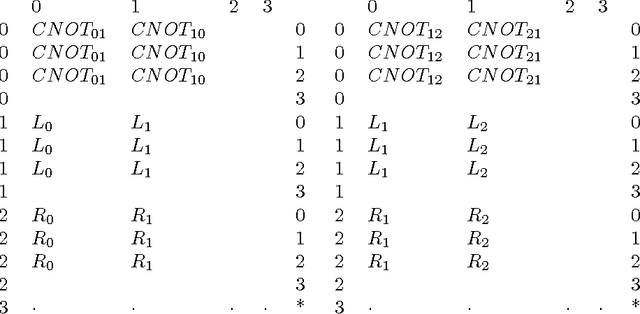
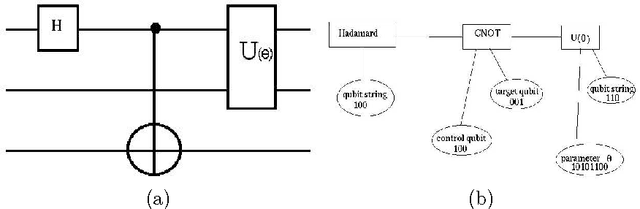
Recently, researchers have applied genetic algorithms (GAs) to address some problems in quantum computation. Also, there has been some works in the designing of genetic algorithms based on quantum theoretical concepts and techniques. The so called Quantum Evolutionary Programming has two major sub-areas: Quantum Inspired Genetic Algorithms (QIGAs) and Quantum Genetic Algorithms (QGAs). The former adopts qubit chromosomes as representations and employs quantum gates for the search of the best solution. The later tries to solve a key question in this field: what GAs will look like as an implementation on quantum hardware? As we shall see, there is not a complete answer for this question. An important point for QGAs is to build a quantum algorithm that takes advantage of both the GA and quantum computing parallelism as well as true randomness provided by quantum computers. In the first part of this paper we present a survey of the main works in GAs plus quantum computing including also our works in this area. Henceforth, we review some basic concepts in quantum computation and GAs and emphasize their inherent parallelism. Next, we review the application of GAs for learning quantum operators and circuit design. Then, quantum evolutionary programming is considered. Finally, we present our current research in this field and some perspectives.