SANGEA: Scalable and Attributed Network Generation

The topic of synthetic graph generators (SGGs) has recently received much attention due to the wave of the latest breakthroughs in generative modelling. However, many state-of-the-art SGGs do not scale well with the graph size. Indeed, in the generation process, all the possible edges for a fixed number of nodes must often be considered, which scales in $\mathcal{O}(N^2)$, with $N$ being the number of nodes in the graph. For this reason, many state-of-the-art SGGs are not applicable to large graphs. In this paper, we present SANGEA, a sizeable synthetic graph generation framework which extends the applicability of any SGG to large graphs. By first splitting the large graph into communities, SANGEA trains one SGG per community, then links the community graphs back together to create a synthetic large graph. Our experiments show that the graphs generated by SANGEA have high similarity to the original graph, in terms of both topology and node feature distribution. Additionally, these generated graphs achieve high utility on downstream tasks such as link prediction. Finally, we provide a privacy assessment of the generated graphs to show that, even though they have excellent utility, they also achieve reasonable privacy scores.

Advancing Reacting Flow Simulations with Data-Driven Models

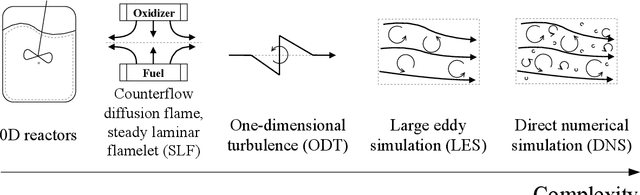
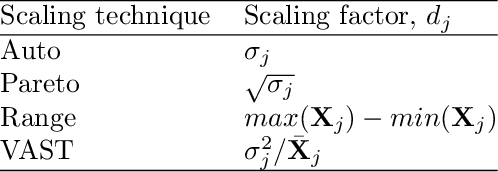
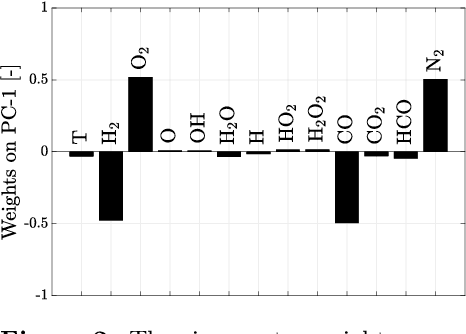
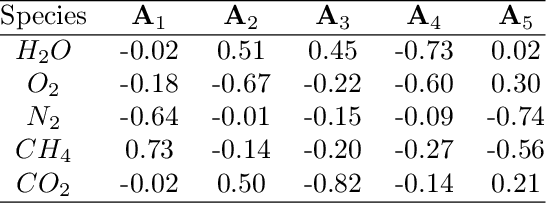
The use of machine learning algorithms to predict behaviors of complex systems is booming. However, the key to an effective use of machine learning tools in multi-physics problems, including combustion, is to couple them to physical and computer models. The performance of these tools is enhanced if all the prior knowledge and the physical constraints are embodied. In other words, the scientific method must be adapted to bring machine learning into the picture, and make the best use of the massive amount of data we have produced, thanks to the advances in numerical computing. The present chapter reviews some of the open opportunities for the application of data-driven reduced-order modeling of combustion systems. Examples of feature extraction in turbulent combustion data, empirical low-dimensional manifold (ELDM) identification, classification, regression, and reduced-order modeling are provided.