A predictive physics-aware hybrid reduced order model for reacting flows

In this work, a new hybrid predictive Reduced Order Model (ROM) is proposed to solve reacting flow problems. This algorithm is based on a dimensionality reduction using Proper Orthogonal Decomposition (POD) combined with deep learning architectures. The number of degrees of freedom is reduced from thousands of temporal points to a few POD modes with their corresponding temporal coefficients. Two different deep learning architectures have been tested to predict the temporal coefficients, based on recursive (RNN) and convolutional (CNN) neural networks. From each architecture, different models have been created to understand the behavior of each parameter of the neural network. Results show that these architectures are able to predict the temporal coefficients of the POD modes, as well as the whole snapshots. The RNN shows lower prediction error for all the variables analyzed. The model was also found capable of predicting more complex simulations showing transfer learning capabilities.

Advancing Reacting Flow Simulations with Data-Driven Models

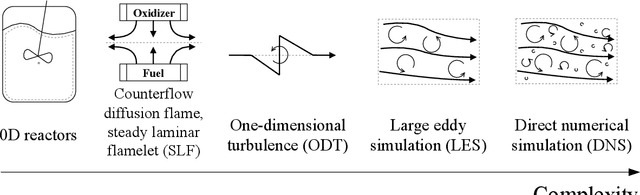
The use of machine learning algorithms to predict behaviors of complex systems is booming. However, the key to an effective use of machine learning tools in multi-physics problems, including combustion, is to couple them to physical and computer models. The performance of these tools is enhanced if all the prior knowledge and the physical constraints are embodied. In other words, the scientific method must be adapted to bring machine learning into the picture, and make the best use of the massive amount of data we have produced, thanks to the advances in numerical computing. The present chapter reviews some of the open opportunities for the application of data-driven reduced-order modeling of combustion systems. Examples of feature extraction in turbulent combustion data, empirical low-dimensional manifold (ELDM) identification, classification, regression, and reduced-order modeling are provided.

Local manifold learning and its link to domain-based physics knowledge

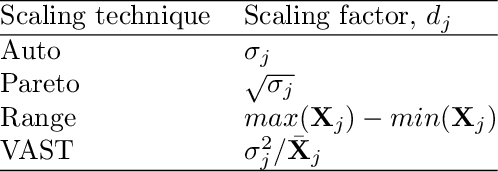
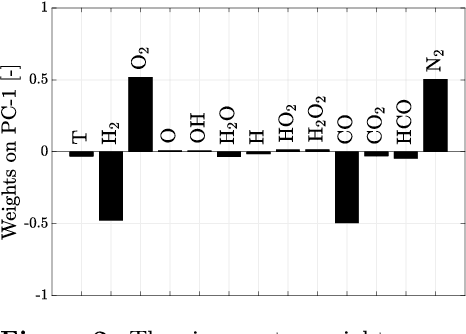
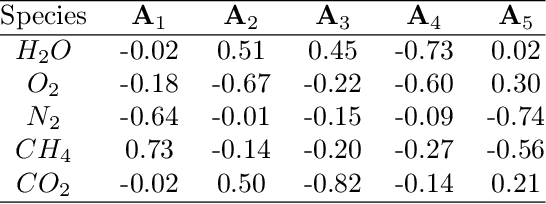
In many reacting flow systems, the thermo-chemical state-space is known or assumed to evolve close to a low-dimensional manifold (LDM). Various approaches are available to obtain those manifolds and subsequently express the original high-dimensional space with fewer parameterizing variables. Principal component analysis (PCA) is one of the dimensionality reduction methods that can be used to obtain LDMs. PCA does not make prior assumptions about the parameterizing variables and retrieves them empirically from the training data. In this paper, we show that PCA applied in local clusters of data (local PCA) is capable of detecting the intrinsic parameterization of the thermo-chemical state-space. We first demonstrate that utilizing three common combustion models of varying complexity: the Burke-Schumann model, the chemical equilibrium model and the homogeneous reactor. Parameterization of these models is known a priori which allows for benchmarking with the local PCA approach. We further extend the application of local PCA to a more challenging case of a turbulent non-premixed $n$-heptane/air jet flame for which the parameterization is no longer obvious. Our results suggest that meaningful parameterization can be obtained also for more complex datasets. We show that local PCA finds variables that can be linked to local stoichiometry, reaction progress and soot formation processes.