Multiplant Nonlinear System Identification by Block-Structured Multikernel Neural Networks in Applications of Interference Cancellation

Problems of linear system identification have closed-form solutions, e.g., using least-squares or maximum-likelihood methods on input-output data. However, already the seemingly simplest problems of nonlinear system identification present more difficulties related to the optimisation of the furrowed error surface. Those cases include the Hammerstein plant with typically a bilinear model representation based on polynomial or Fourier expansion of its nonlinear element. Wiener plants induce actual nonlinearity in the parameters, which further complicates the optimisation. Neural network models and related optimisers are, however, well-prepared to represent and solve nonlinear problems. Unfortunately, the available data for nonlinear system identification might be too diverse to support accurate and consistent model representation. This diversity may refer to different impulse responses and nonlinear functions that arise in different measurements of (different) plants. We therefore propose multikernel neural network models to represent nonlinear plants with a subset of trainable weights shared between different measurements and another subset of plant-specific (i.e., multikernel) weights to adhere to the characteristics of specific measurements. We demonstrate that in this way we can fit neural network models to the diverse data which cannot be done with some standard methods of nonlinear system identification. For model testing, the subset of shared weights of the entire trained model is reused to support the identification and representation of unseen plant measurements, while the plant-specific model weights are readjusted to specifically meet the test data.

On Neural-Network Representation of Wireless Self-Interference for Inband Full-Duplex Communications

Neural network modeling is a key technology of science and research and a platform for deployment of algorithms to systems. In wireless communications, system modeling plays a pivotal role for interference cancellation with specifically high requirements of accuracy regarding the elimination of self-interference in full-duplex relays. This paper hence investigates the potential of identification and representation of the self-interference channel by neural network architectures. The approach is promising for its ability to cope with nonlinear representations, but the variability of channel characteristics is a first obstacle in straightforward application of data-driven neural networks. We therefore propose architectures with a touch of "adaptivity" to accomplish a successful training. For reproducibility of results and further investigations with possibly stronger models and enhanced performance, we document and share our data.

Control Architecture of the Double-Cross-Correlation Processor for Sampling-Rate-Offset Estimation in Acoustic Sensor Networks

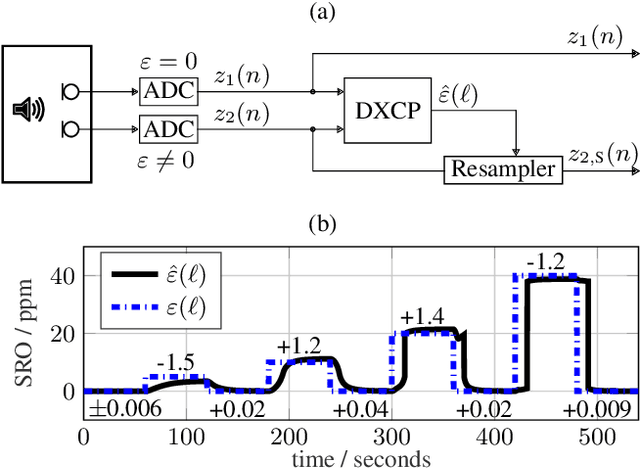
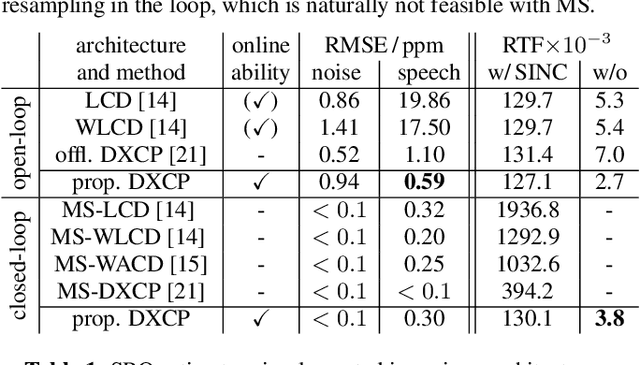
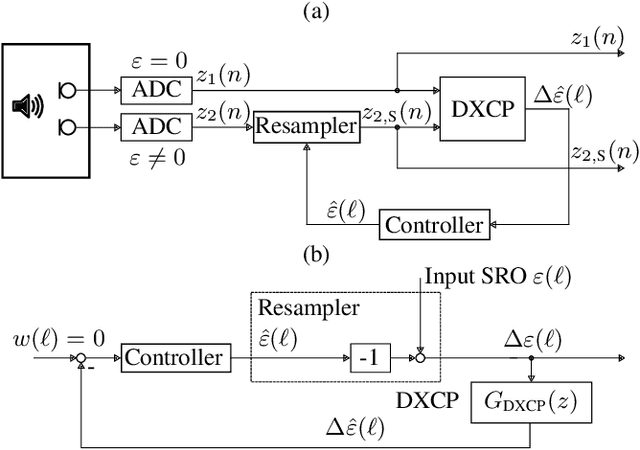
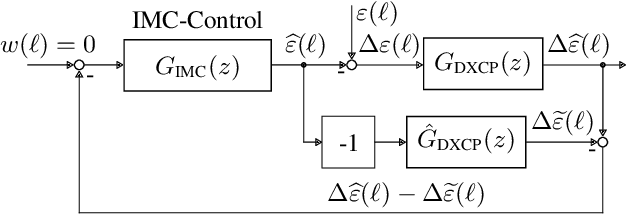
Distributed hardware of acoustic sensor networks bears inconsistency of local sampling frequencies, which is detrimental to signal processing. Fundamentally, sampling rate offset (SRO) nonlinearly relates the discrete-time signals acquired by different sensor nodes. As such, retrieval of SRO from the available signals requires nonlinear estimation, like double-cross-correlation processing (DXCP), and frequently results in biased estimation. SRO compensation by asynchronous sampling rate conversion (ASRC) on the signals then leaves an unacceptable residual. As a remedy to this problem, multi-stage procedures have been devised to diminish the SRO residual with multiple iterations of SRO estimation and ASRC over the entire signal. This paper converts the mechanism of offline multi-stage processing into a continuous feedback-control loop comprising a controlled ASRC unit followed by an online implementation of DXCP-based SRO estimation. To support the design of an optimum internal model control unit for this closed-loop system, the paper deploys an analytical dynamical model of the proposed online DXCP. The resulting control architecture then merely applies a single treatment of each signal frame, while efficiently diminishing SRO bias with time. Evaluations with both speech and Gaussian input demonstrate that the high accuracy of multi-stage processing is maintained at the low complexity of single-stage (open-loop) processing.