Predictive Density Combination Using a Tree-Based Synthesis Function

Bayesian predictive synthesis (BPS) provides a method for combining multiple predictive distributions based on agent/expert opinion analysis theory and encompasses a range of existing density forecast pooling methods. The key ingredient in BPS is a ``synthesis'' function. This is typically specified parametrically as a dynamic linear regression. In this paper, we develop a nonparametric treatment of the synthesis function using regression trees. We show the advantages of our tree-based approach in two macroeconomic forecasting applications. The first uses density forecasts for GDP growth from the euro area's Survey of Professional Forecasters. The second combines density forecasts of US inflation produced by many regression models involving different predictors. Both applications demonstrate the benefits -- in terms of improved forecast accuracy and interpretability -- of modeling the synthesis function nonparametrically.

Approximate Bayesian inference and forecasting in huge-dimensional multi-country VARs

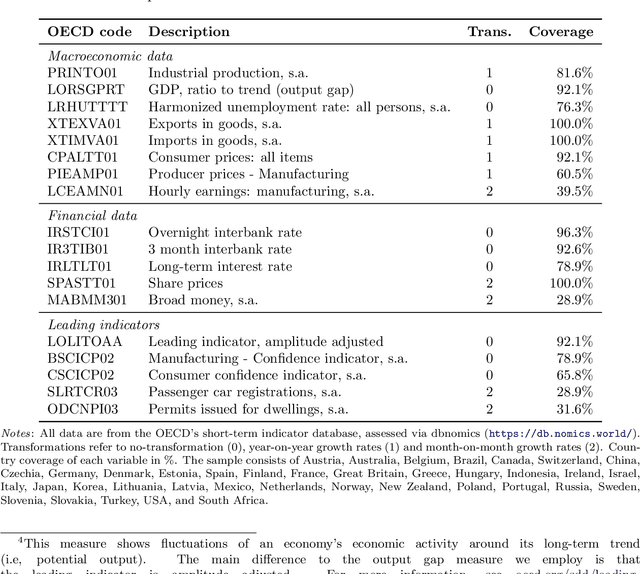
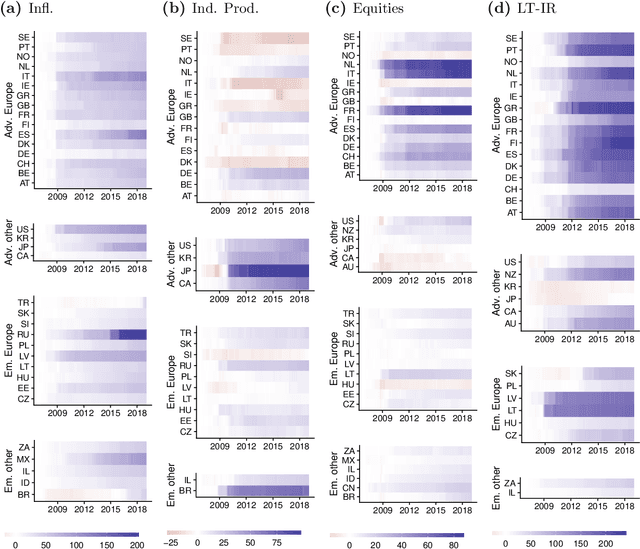
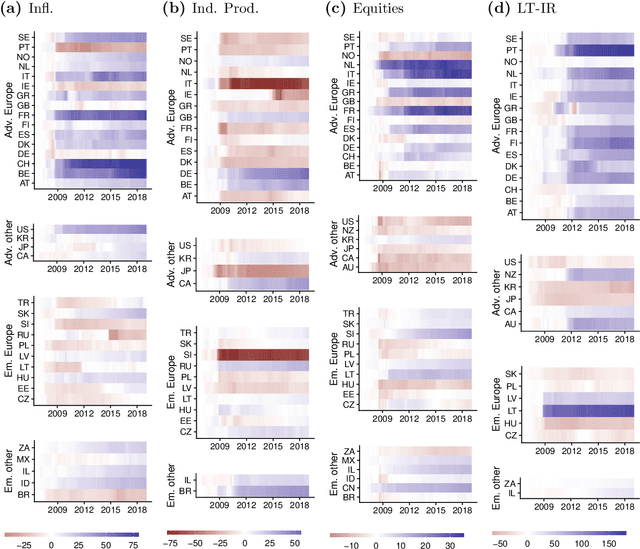
The Panel Vector Autoregressive (PVAR) model is a popular tool for macroeconomic forecasting and structural analysis in multi-country applications since it allows for spillovers between countries in a very flexible fashion. However, this flexibility means that the number of parameters to be estimated can be enormous leading to over-parameterization concerns. Bayesian global-local shrinkage priors, such as the Horseshoe prior used in this paper, can overcome these concerns, but they require the use of Markov Chain Monte Carlo (MCMC) methods rendering them computationally infeasible in high dimensions. In this paper, we develop computationally efficient Bayesian methods for estimating PVARs using an integrated rotated Gaussian approximation (IRGA). This exploits the fact that whereas own country information is often important in PVARs, information on other countries is often unimportant. Using an IRGA, we split the the posterior into two parts: one involving own country coefficients, the other involving other country coefficients. Fast methods such as approximate message passing or variational Bayes can be used on the latter and, conditional on these, the former are estimated with precision using MCMC methods. In a forecasting exercise involving PVARs with up to $18$ variables for each of $38$ countries, we demonstrate that our methods produce good forecasts quickly.

Nowcasting in a Pandemic using Non-Parametric Mixed Frequency VARs

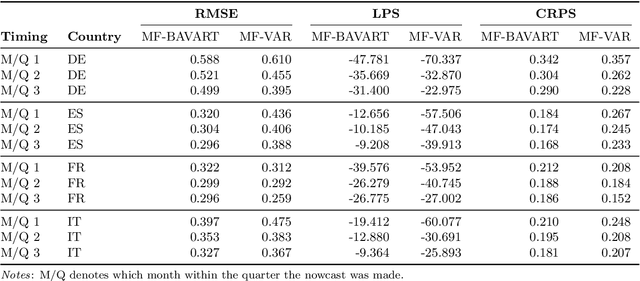
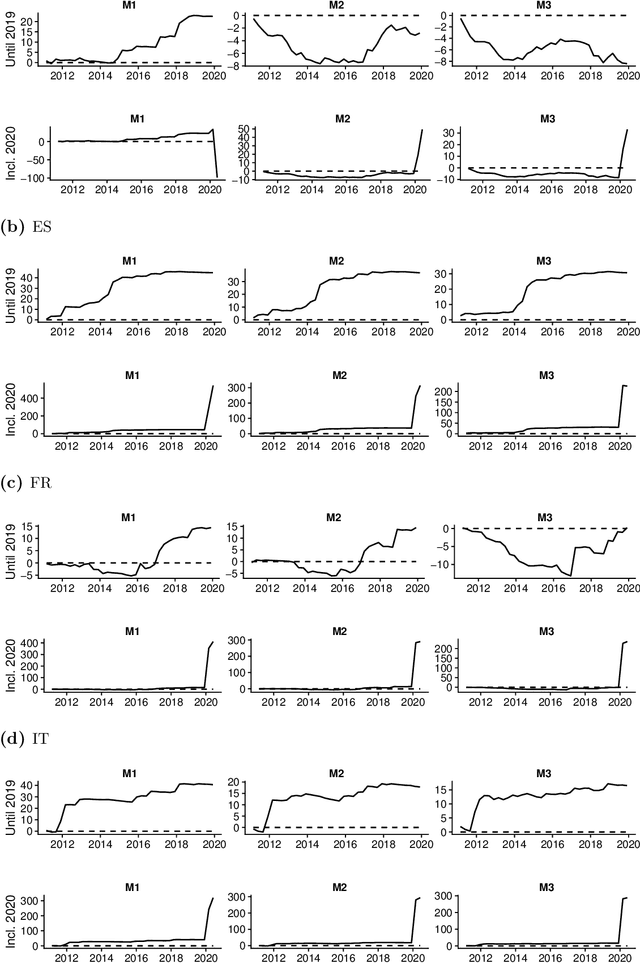
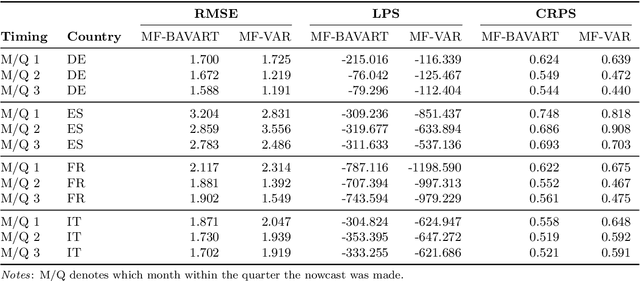
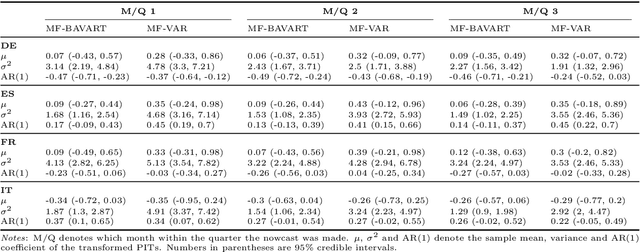
This paper develops Bayesian econometric methods for posterior and predictive inference in a non-parametric mixed frequency VAR using additive regression trees. We argue that regression tree models are ideally suited for macroeconomic nowcasting in the face of the extreme observations produced by the pandemic due to their flexibility and ability to model outliers. In a nowcasting application involving four major countries in the European Union, we find substantial improvements in nowcasting performance relative to a linear mixed frequency VAR. A detailed examination of the predictive densities in the first six months of 2020 shows where these improvements are achieved.