Vectorial Parameterizations of Pose

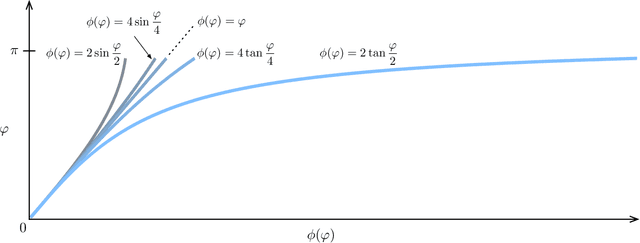
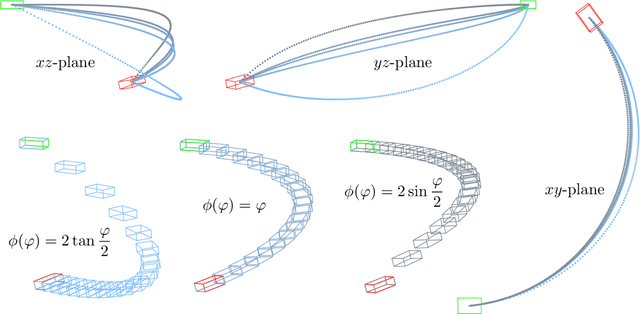
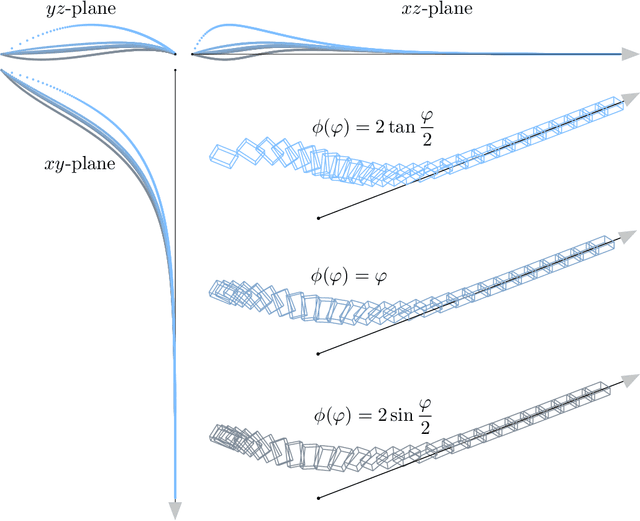
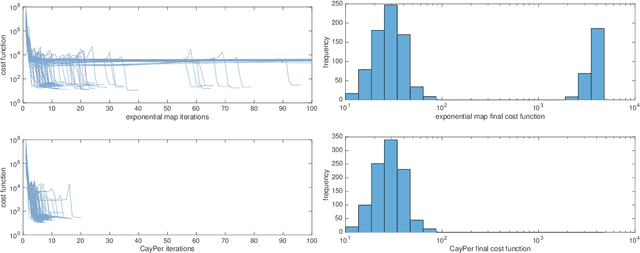
Robotics and computer vision problems commonly require handling rigid-body motions comprising translation and rotation - together referred to as pose. In some situations, a vectorial parameterization of pose can be useful, where elements of a vector space are surjectively mapped to a matrix Lie group. For example, these vectorial representations can be employed for optimization as well as uncertainty representation on groups. The most common mapping is the matrix exponential, which maps elements of a Lie algebra onto the associated Lie group. However, this choice is not unique. It has been previously shown how to characterize all such vectorial parameterizations for SO(3), the group of rotations. We extend this result to SE(3), the group of poses (translation and rotation), showing how to build a family of mappings that includes the matrix exponential as well as the Cayley transformation. While our main contribution is the theory, we also demonstrate three different applications of the proposed pose mappings: (i) pose interpolation, (ii) pose servoing control, and (iii) pose estimation in a pointcloud alignment problem. In the pointcloud alignment problem our results lead to a new algorithm based on the Cayley transformation, which we call CayPer.

Variational Inference as Iterative Projection in a Bayesian Hilbert Space

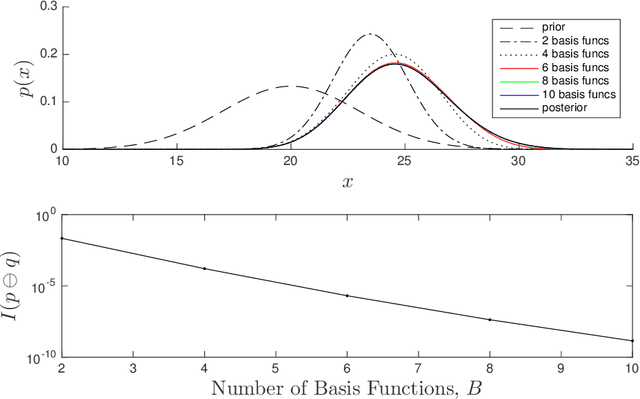
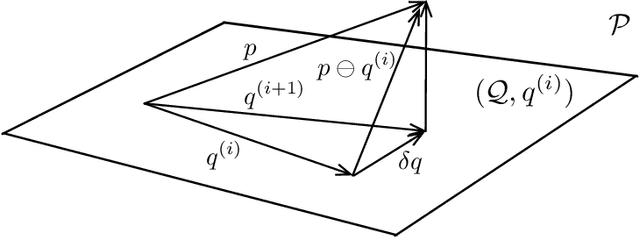
Variational Bayesian inference is an important machine-learning tool that finds application from statistics to robotics. The goal is to find an approximate probability density function (PDF) from a chosen family that is in some sense `closest' to the full Bayesian posterior. Closeness is typically defined through the selection of an appropriate loss functional such as the Kullback-Leibler (KL) divergence. In this paper, we explore a new formulation of variational inference by exploiting the fact that the set of PDFs constitutes a Bayesian Hilbert space under careful definitions of vector addition, scalar multiplication and an inner product. We show that variational inference based on KL divergence then amounts to an iterative projection of the Bayesian posterior onto a subspace corresponding to the selected approximation family. In fact, the inner product chosen for the Bayesian Hilbert space suggests the definition of a new measure of the information contained in a PDF and in turn a new divergence is introduced. Each step in the iterative projection is equivalent to a local minimization of this divergence. We present an example Bayesian subspace based on exponentiated Hermite polynomials as well as work through the details of this general framework for the specific case of the multivariate Gaussian approximation family and show the equivalence to another Gaussian variational inference approach. We furthermore discuss the implications for systems that exhibit sparsity, which is handled naturally in Bayesian space.

Autonomous Multirobot Excavation for Lunar Applications

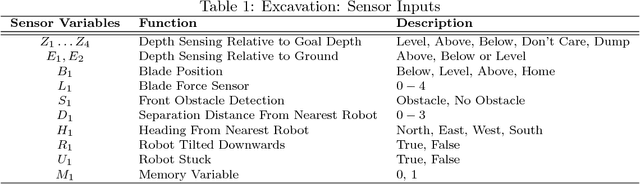
In this paper, a control approach called Artificial Neural Tissue (ANT) is applied to multirobot excavation for lunar base preparation tasks including clearing landing pads and burying of habitat modules. We show for the first time, a team of autonomous robots excavating a terrain to match a given 3D blueprint. Constructing mounds around landing pads will provide physical shielding from debris during launch/landing. Burying a human habitat modules under 0.5 m of lunar regolith is expected to provide both radiation shielding and maintain temperatures of -25 $^{o}$C. This minimizes base life-support complexity and reduces launch mass. ANT is compelling for a lunar mission because it doesn't require a team of astronauts for excavation and it requires minimal supervision. The robot teams are shown to autonomously interpret blueprints, excavate and prepare sites for a lunar base. Because little pre-programmed knowledge is provided, the controllers discover creative techniques. ANT evolves techniques such as slot-dozing that would otherwise require excavation experts. This is critical in making an excavation mission feasible when it is prohibitively expensive to send astronauts. The controllers evolve elaborate negotiation behaviors to work in close quarters. These and other techniques such as concurrent evolution of the controller and team size are shown to tackle problem of antagonism, when too many robots interfere reducing the overall efficiency or worse, resulting in gridlock. While many challenges remain with this technology our work shows a compelling pathway for field testing this approach.