Variational Inference as Iterative Projection in a Bayesian Hilbert Space

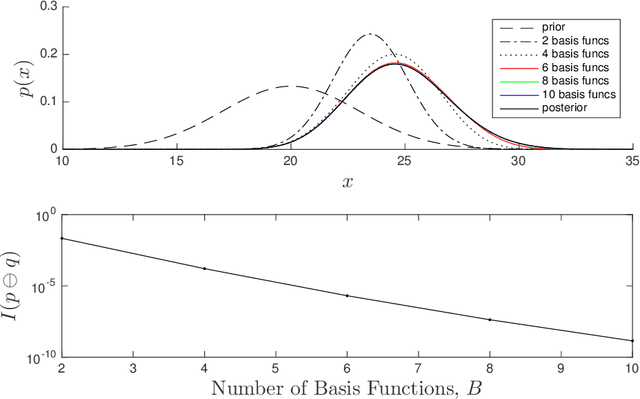
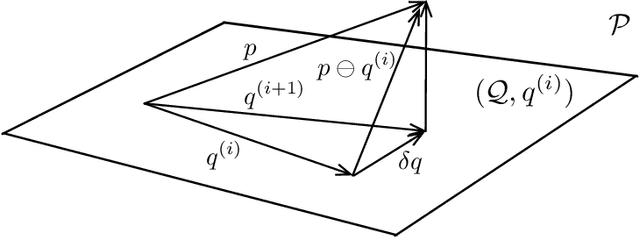
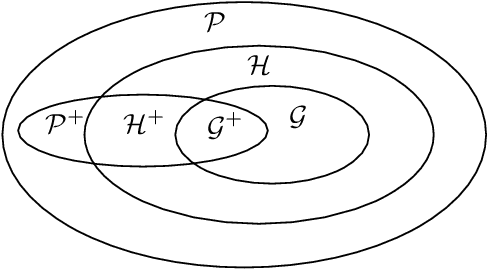
Variational Bayesian inference is an important machine-learning tool that finds application from statistics to robotics. The goal is to find an approximate probability density function (PDF) from a chosen family that is in some sense `closest' to the full Bayesian posterior. Closeness is typically defined through the selection of an appropriate loss functional such as the Kullback-Leibler (KL) divergence. In this paper, we explore a new formulation of variational inference by exploiting the fact that the set of PDFs constitutes a Bayesian Hilbert space under careful definitions of vector addition, scalar multiplication and an inner product. We show that variational inference based on KL divergence then amounts to an iterative projection of the Bayesian posterior onto a subspace corresponding to the selected approximation family. In fact, the inner product chosen for the Bayesian Hilbert space suggests the definition of a new measure of the information contained in a PDF and in turn a new divergence is introduced. Each step in the iterative projection is equivalent to a local minimization of this divergence. We present an example Bayesian subspace based on exponentiated Hermite polynomials as well as work through the details of this general framework for the specific case of the multivariate Gaussian approximation family and show the equivalence to another Gaussian variational inference approach. We furthermore discuss the implications for systems that exhibit sparsity, which is handled naturally in Bayesian space.