FEMDA: a unified framework for discriminant analysis

Although linear and quadratic discriminant analysis are widely recognized classical methods, they can encounter significant challenges when dealing with non-Gaussian distributions or contaminated datasets. This is primarily due to their reliance on the Gaussian assumption, which lacks robustness. We first explain and review the classical methods to address this limitation and then present a novel approach that overcomes these issues. In this new approach, the model considered is an arbitrary Elliptically Symmetrical (ES) distribution per cluster with its own arbitrary scale parameter. This flexible model allows for potentially diverse and independent samples that may not follow identical distributions. By deriving a new decision rule, we demonstrate that maximum-likelihood parameter estimation and classification are simple, efficient, and robust compared to state-of-the-art methods.

Algorithme EM régularisé

Expectation-Maximization (EM) algorithm is a widely used iterative algorithm for computing maximum likelihood estimate when dealing with Gaussian Mixture Model (GMM). When the sample size is smaller than the data dimension, this could lead to a singular or poorly conditioned covariance matrix and, thus, to performance reduction. This paper presents a regularized version of the EM algorithm that efficiently uses prior knowledge to cope with a small sample size. This method aims to maximize a penalized GMM likelihood where regularized estimation may ensure positive definiteness of covariance matrix updates by shrinking the estimators towards some structured target covariance matrices. Finally, experiments on real data highlight the good performance of the proposed algorithm for clustering purposes

FEMDA: Une méthode de classification robuste et flexible

Linear and Quadratic Discriminant Analysis (LDA and QDA) are well-known classical methods but can heavily suffer from non-Gaussian distributions and/or contaminated datasets, mainly because of the underlying Gaussian assumption that is not robust. This paper studies the robustness to scale changes in the data of a new discriminant analysis technique where each data point is drawn by its own arbitrary Elliptically Symmetrical (ES) distribution and its own arbitrary scale parameter. Such a model allows for possibly very heterogeneous, independent but non-identically distributed samples. The new decision rule derived is simple, fast, and robust to scale changes in the data compared to other state-of-the-art method

Regularized EM algorithm

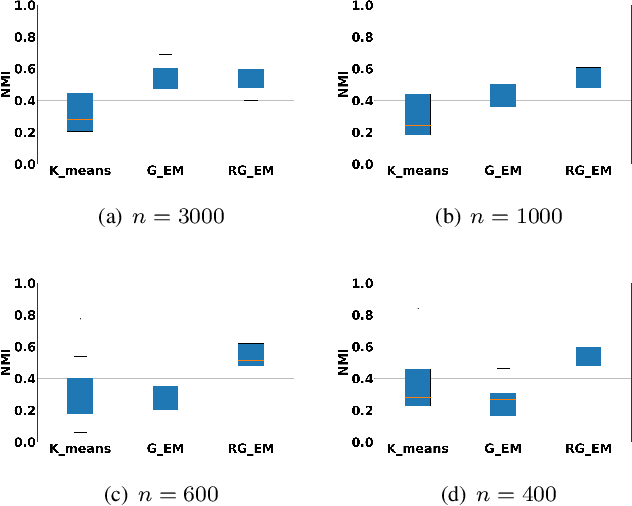
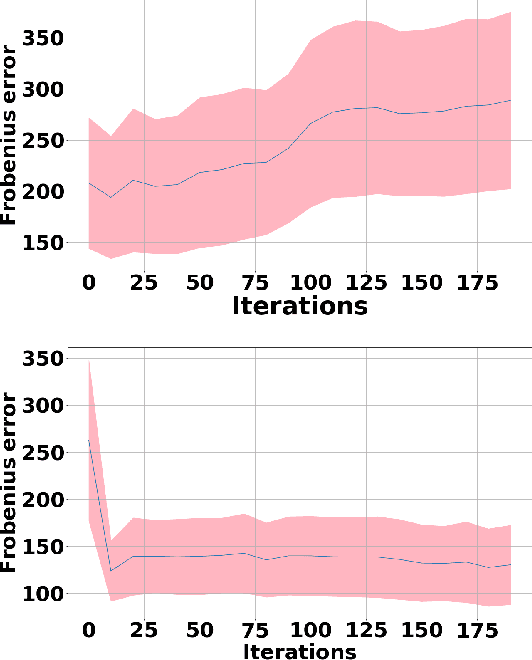
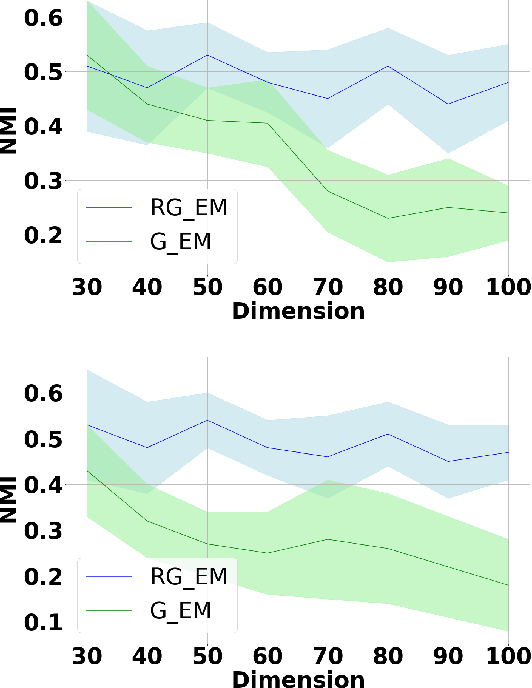
Expectation-Maximization (EM) algorithm is a widely used iterative algorithm for computing (local) maximum likelihood estimate (MLE). It can be used in an extensive range of problems, including the clustering of data based on the Gaussian mixture model (GMM). Numerical instability and convergence problems may arise in situations where the sample size is not much larger than the data dimensionality. In such low sample support (LSS) settings, the covariance matrix update in the EM-GMM algorithm may become singular or poorly conditioned, causing the algorithm to crash. On the other hand, in many signal processing problems, a priori information can be available indicating certain structures for different cluster covariance matrices. In this paper, we present a regularized EM algorithm for GMM-s that can make efficient use of such prior knowledge as well as cope with LSS situations. The method aims to maximize a penalized GMM likelihood where regularized estimation may be used to ensure positive definiteness of covariance matrix updates and shrink the estimators towards some structured target covariance matrices. We show that the theoretical guarantees of convergence hold, leading to better performing EM algorithm for structured covariance matrix models or with low sample settings.

M-estimators of scatter with eigenvalue shrinkage

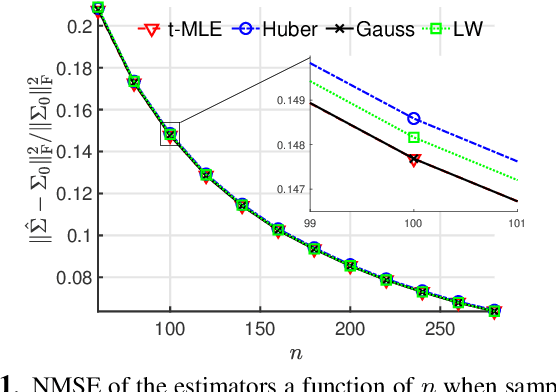
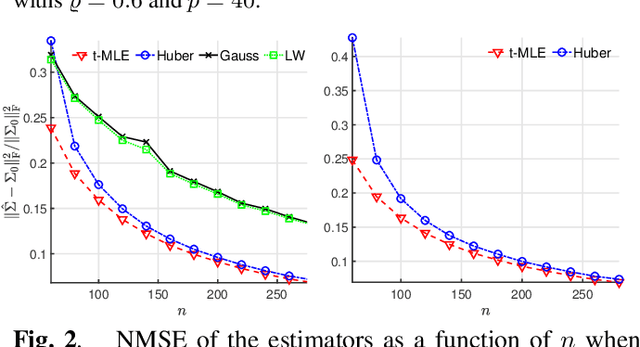
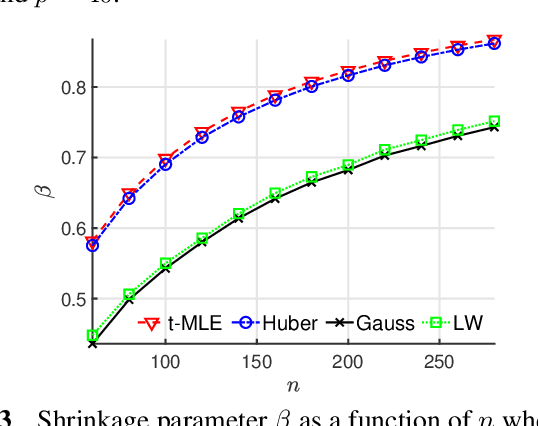
A popular regularized (shrinkage) covariance estimator is the shrinkage sample covariance matrix (SCM) which shares the same set of eigenvectors as the SCM but shrinks its eigenvalues toward its grand mean. In this paper, a more general approach is considered in which the SCM is replaced by an M-estimator of scatter matrix and a fully automatic data adaptive method to compute the optimal shrinkage parameter with minimum mean squared error is proposed. Our approach permits the use of any weight function such as Gaussian, Huber's, or $t$ weight functions, all of which are commonly used in M-estimation framework. Our simulation examples illustrate that shrinkage M-estimators based on the proposed optimal tuning combined with robust weight function do not loose in performance to shrinkage SCM estimator when the data is Gaussian, but provide significantly improved performance when the data is sampled from a heavy-tailed distribution.