Regularized EM algorithm
Paper and Code
Mar 27, 2023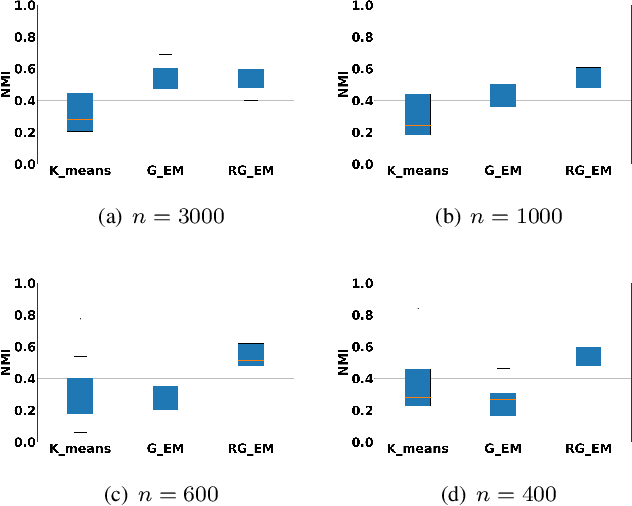
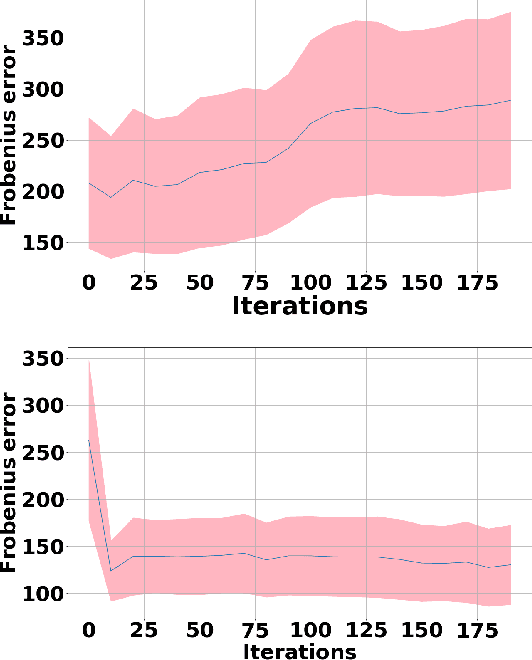
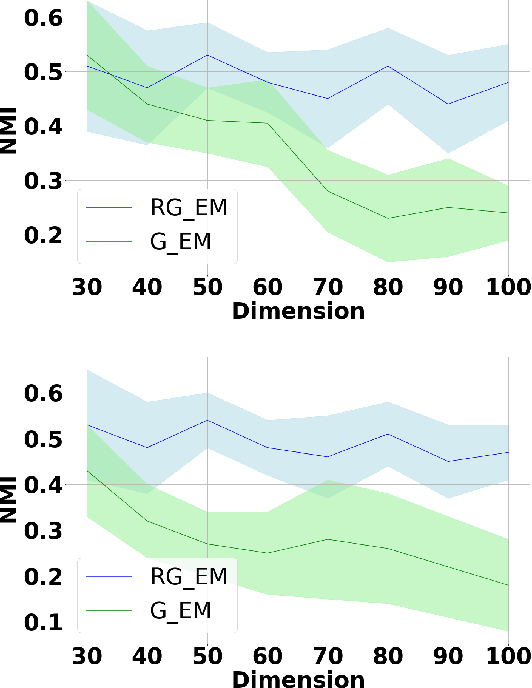
Expectation-Maximization (EM) algorithm is a widely used iterative algorithm for computing (local) maximum likelihood estimate (MLE). It can be used in an extensive range of problems, including the clustering of data based on the Gaussian mixture model (GMM). Numerical instability and convergence problems may arise in situations where the sample size is not much larger than the data dimensionality. In such low sample support (LSS) settings, the covariance matrix update in the EM-GMM algorithm may become singular or poorly conditioned, causing the algorithm to crash. On the other hand, in many signal processing problems, a priori information can be available indicating certain structures for different cluster covariance matrices. In this paper, we present a regularized EM algorithm for GMM-s that can make efficient use of such prior knowledge as well as cope with LSS situations. The method aims to maximize a penalized GMM likelihood where regularized estimation may be used to ensure positive definiteness of covariance matrix updates and shrink the estimators towards some structured target covariance matrices. We show that the theoretical guarantees of convergence hold, leading to better performing EM algorithm for structured covariance matrix models or with low sample settings.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge