An Analysis on the Effects of Evolving the Monte Carlo Tree Search Upper Confidence for Trees Selection Policy on Unimodal, Multimodal and Deceptive Landscapes

Monte Carlo Tree Search (MCTS) is a best-first sampling method employed in the search for optimal decisions. The effectiveness of MCTS relies on the construction of its statistical tree, with the selection policy playing a crucial role. A selection policy that works particularly well in MCTS is the Upper Confidence Bounds for Trees, referred to as UCT. The research community has also put forth more sophisticated bounds aimed at enhancing MCTS performance on specific problem domains. Thus, while MCTS UCT generally performs well, there may be variants that outperform it. This has led to various efforts to evolve selection policies for use in MCTS. While all of these previous works are inspiring, none have undertaken an in-depth analysis to shed light on the circumstances in which an evolved alternative to MCTS UCT might prove advantageous. Most of these studies have focused on a single type of problem. In sharp contrast, this work explores the use of five functions of different natures, ranging from unimodal to multimodal and deceptive functions. We illustrate how the evolution of MCTS UCT can yield benefits in multimodal and deceptive scenarios, whereas MCTS UCT is robust in all of the functions used in this work.

Towards Understanding the Effects of Evolving the MCTS UCT Selection Policy

Monte Carlo Tree Search (MCTS) is a sampling best-first method to search for optimal decisions. The success of MCTS depends heavily on how the MCTS statistical tree is built and the selection policy plays a fundamental role in this. A particular selection policy that works particularly well, widely adopted in MCTS, is the Upper Confidence Bounds for Trees, referred to as UCT. Other more sophisticated bounds have been proposed by the community with the goal to improve MCTS performance on particular problems. Thus, it is evident that while the MCTS UCT behaves generally well, some variants might behave better. As a result of this, multiple works have been proposed to evolve a selection policy to be used in MCTS. Although all these works are inspiring, none of them have carried out an in-depth analysis shedding light under what circumstances an evolved alternative of MCTS UCT might be beneficial in MCTS due to focusing on a single type of problem. In sharp contrast to this, in this work we use five functions of different nature, going from a unimodal function, covering multimodal functions to deceptive functions. We demonstrate how the evolution of the MCTS UCT might be beneficial in multimodal and deceptive scenarios, whereas the MCTS UCT is robust in unimodal scenarios and competitive in the rest of the scenarios used in this study.

Evolving the MCTS Upper Confidence Bounds for Trees Using a Semantic-inspired Evolutionary Algorithm in the Game of Carcassonne

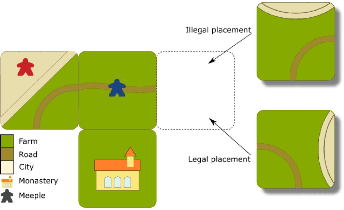
Monte Carlo Tree Search (MCTS) is a sampling best-first method to search for optimal decisions. The success of MCTS depends heavily on how the tree is built and the selection process plays a fundamental role in this. One particular selection mechanism that has proved to be reliable is based on the Upper Confidence Bounds for Trees (UCT). The UCT attempts to balance exploration and exploitation by considering the values stored in the statistical tree of the MCTS. However, some tuning of the MCTS UCT is necessary for this to work well. In this work, we use Evolutionary Algorithms (EAs) to evolve mathematical expressions with the goal to substitute the UCT formula and use the evolved expressions in MCTS. More specifically, we evolve expressions by means of our proposed Semantic-inspired Evolutionary Algorithm in MCTS approach (SIEA-MCTS). This is inspired by semantics in Genetic Programming (GP), where the use of fitness cases is seen as a requirement to be adopted in GP. Fitness cases are normally used to determine the fitness of individuals and can be used to compute the semantic similarity (or dissimilarity) of individuals. However, fitness cases are not available in MCTS. We extend this notion by using multiple reward values from MCTS that allow us to determine both the fitness of an individual and its semantics. By doing so, we show how SIEA-MCTS is able to successfully evolve mathematical expressions that yield better or competitive results compared to UCT without the need of tuning these evolved expressions. We compare the performance of the proposed SIEA-MCTS against MCTS algorithms, MCTS Rapid Action Value Estimation algorithms, three variants of the *-minimax family of algorithms, a random controller and two more EA approaches. We consistently show how SIEA-MCTS outperforms most of these intelligent controllers in the challenging game of Carcassonne.

Playing Carcassonne with Monte Carlo Tree Search

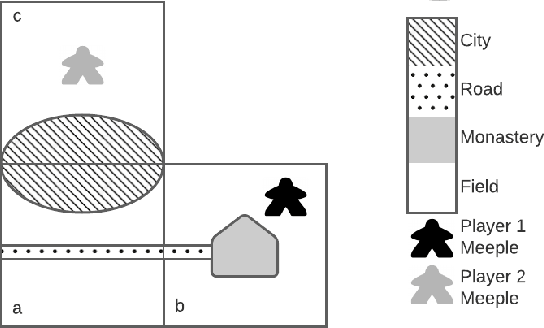
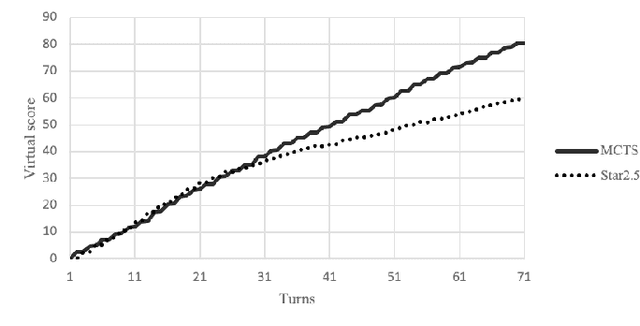
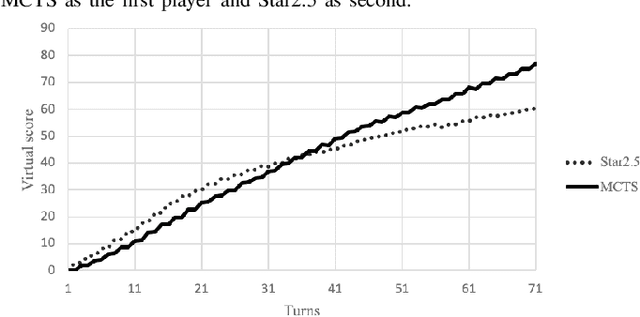
Monte Carlo Tree Search (MCTS) is a relatively new sampling method with multiple variants in the literature. They can be applied to a wide variety of challenging domains including board games, video games, and energy-based problems to mention a few. In this work, we explore the use of the vanilla MCTS and the MCTS with Rapid Action Value Estimation (MCTS-RAVE) in the game of Carcassonne, a stochastic game with a deceptive scoring system where limited research has been conducted. We compare the strengths of the MCTS-based methods with the Star2.5 algorithm, previously reported to yield competitive results in the game of Carcassonne when a domain-specific heuristic is used to evaluate the game states. We analyse the particularities of the strategies adopted by the algorithms when they share a common reward system. The MCTS-based methods consistently outperformed the Star2.5 algorithm given their ability to find and follow long-term strategies, with the vanilla MCTS exhibiting a more robust game-play than the MCTS-RAVE.

Statistical Tree-based Population Seeding for Rolling Horizon EAs in General Video Game Playing

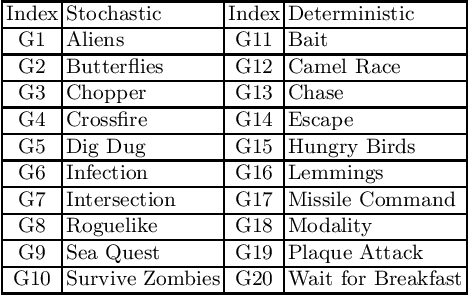
Multiple Artificial Intelligence (AI) methods have been proposed over recent years to create controllers to play multiple video games of different nature and complexity without revealing the specific mechanics of each of these games to the AI methods. In recent years, Evolutionary Algorithms (EAs) employing rolling horizon mechanisms have achieved extraordinary results in these type of problems. However, some limitations are present in Rolling Horizon EAs making it a grand challenge of AI. These limitations include the wasteful mechanism of creating a population and evolving it over a fraction of a second to propose an action to be executed by the game agent. Another limitation is to use a scalar value (fitness value) to direct evolutionary search instead of accounting for a mechanism that informs us how a particular agent behaves during the rolling horizon simulation. In this work, we address both of these issues. We introduce the use of a statistical tree that tackles the latter limitation. Furthermore, we tackle the former limitation by employing a mechanism that allows us to seed part of the population using Monte Carlo Tree Search, a method that has dominated multiple General Video Game AI competitions. We show how the proposed novel mechanism, called Statistical Tree-based Population Seeding, achieves better results compared to vanilla Rolling Horizon EAs in a set of 20 games, including 10 stochastic and 10 deterministic games.