Algorithmic learning of probability distributions from random data in the limit

We study the problem of identifying a probability distribution for some given randomly sampled data in the limit, in the context of algorithmic learning theory as proposed recently by Vinanyi and Chater. We show that there exists a computable partial learner for the computable probability measures, while by Bienvenu, Monin and Shen it is known that there is no computable learner for the computable probability measures. Our main result is the characterization of the oracles that compute explanatory learners for the computable (continuous) probability measures as the high oracles. This provides an analogue of a well-known result of Adleman and Blum in the context of learning computable probability distributions. We also discuss related learning notions such as behaviorally correct learning and orther variations of explanatory learning, in the context of learning probability distributions from data.

Combining Models of Approximation with Partial Learning

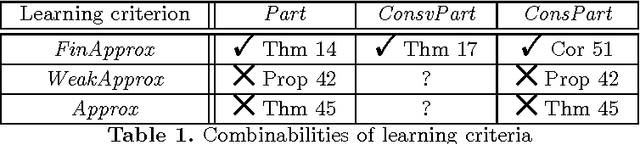
In Gold's framework of inductive inference, the model of partial learning requires the learner to output exactly one correct index for the target object and only the target object infinitely often. Since infinitely many of the learner's hypotheses may be incorrect, it is not obvious whether a partial learner can be modifed to "approximate" the target object. Fulk and Jain (Approximate inference and scientific method. Information and Computation 114(2):179--191, 1994) introduced a model of approximate learning of recursive functions. The present work extends their research and solves an open problem of Fulk and Jain by showing that there is a learner which approximates and partially identifies every recursive function by outputting a sequence of hypotheses which, in addition, are also almost all finite variants of the target function. The subsequent study is dedicated to the question how these findings generalise to the learning of r.e. languages from positive data. Here three variants of approximate learning will be introduced and investigated with respect to the question whether they can be combined with partial learning. Following the line of Fulk and Jain's research, further investigations provide conditions under which partial language learners can eventually output only finite variants of the target language. The combinabilities of other partial learning criteria will also be briefly studied.