Combining Models of Approximation with Partial Learning
Paper and Code
Jul 23, 2015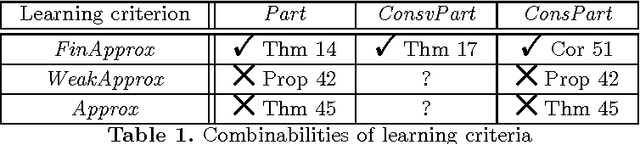
In Gold's framework of inductive inference, the model of partial learning requires the learner to output exactly one correct index for the target object and only the target object infinitely often. Since infinitely many of the learner's hypotheses may be incorrect, it is not obvious whether a partial learner can be modifed to "approximate" the target object. Fulk and Jain (Approximate inference and scientific method. Information and Computation 114(2):179--191, 1994) introduced a model of approximate learning of recursive functions. The present work extends their research and solves an open problem of Fulk and Jain by showing that there is a learner which approximates and partially identifies every recursive function by outputting a sequence of hypotheses which, in addition, are also almost all finite variants of the target function. The subsequent study is dedicated to the question how these findings generalise to the learning of r.e. languages from positive data. Here three variants of approximate learning will be introduced and investigated with respect to the question whether they can be combined with partial learning. Following the line of Fulk and Jain's research, further investigations provide conditions under which partial language learners can eventually output only finite variants of the target language. The combinabilities of other partial learning criteria will also be briefly studied.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge