Monte Carlo Search Algorithm Discovery for One Player Games

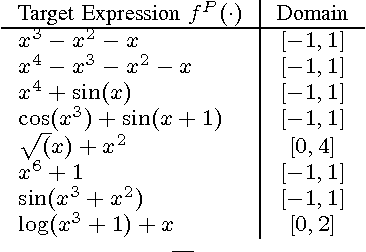
Much current research in AI and games is being devoted to Monte Carlo search (MCS) algorithms. While the quest for a single unified MCS algorithm that would perform well on all problems is of major interest for AI, practitioners often know in advance the problem they want to solve, and spend plenty of time exploiting this knowledge to customize their MCS algorithm in a problem-driven way. We propose an MCS algorithm discovery scheme to perform this in an automatic and reproducible way. We first introduce a grammar over MCS algorithms that enables inducing a rich space of candidate algorithms. Afterwards, we search in this space for the algorithm that performs best on average for a given distribution of training problems. We rely on multi-armed bandits to approximately solve this optimization problem. The experiments, generated on three different domains, show that our approach enables discovering algorithms that outperform several well-known MCS algorithms such as Upper Confidence bounds applied to Trees and Nested Monte Carlo search. We also show that the discovered algorithms are generally quite robust with respect to changes in the distribution over the training problems.

Optimized Look-Ahead Tree Policies: A Bridge Between Look-Ahead Tree Policies and Direct Policy Search

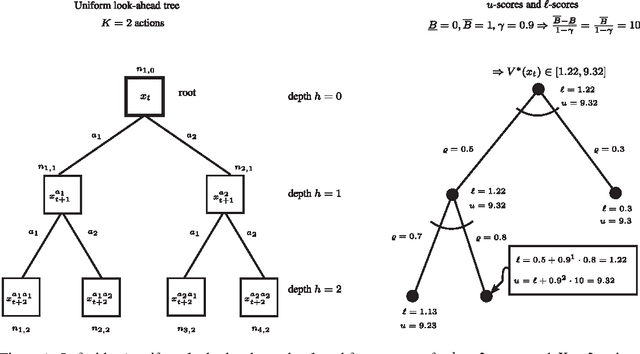
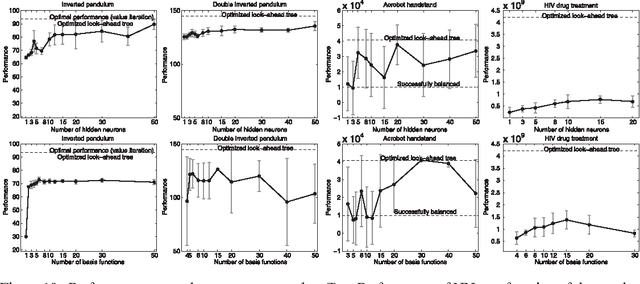
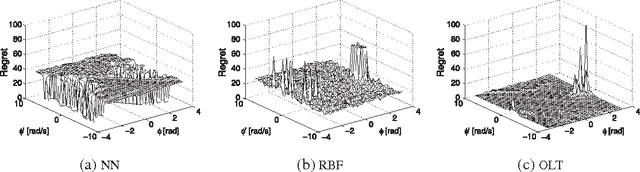
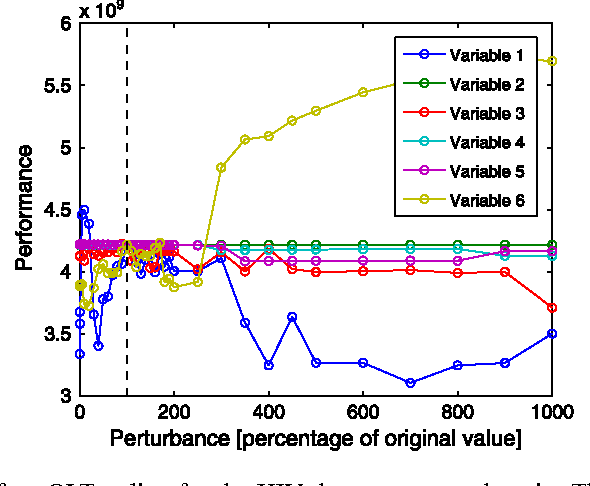
Direct policy search (DPS) and look-ahead tree (LT) policies are two widely used classes of techniques to produce high performance policies for sequential decision-making problems. To make DPS approaches work well, one crucial issue is to select an appropriate space of parameterized policies with respect to the targeted problem. A fundamental issue in LT approaches is that, to take good decisions, such policies must develop very large look-ahead trees which may require excessive online computational resources. In this paper, we propose a new hybrid policy learning scheme that lies at the intersection of DPS and LT, in which the policy is an algorithm that develops a small look-ahead tree in a directed way, guided by a node scoring function that is learned through DPS. The LT-based representation is shown to be a versatile way of representing policies in a DPS scheme, while at the same time, DPS enables to significantly reduce the size of the look-ahead trees that are required to take high-quality decisions. We experimentally compare our method with two other state-of-the-art DPS techniques and four common LT policies on four benchmark domains and show that it combines the advantages of the two techniques from which it originates. In particular, we show that our method: (1) produces overall better performing policies than both pure DPS and pure LT policies, (2) requires a substantially smaller number of policy evaluations than other DPS techniques, (3) is easy to tune and (4) results in policies that are quite robust with respect to perturbations of the initial conditions.

Meta-Learning of Exploration/Exploitation Strategies: The Multi-Armed Bandit Case

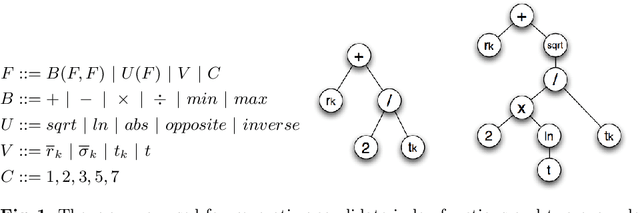
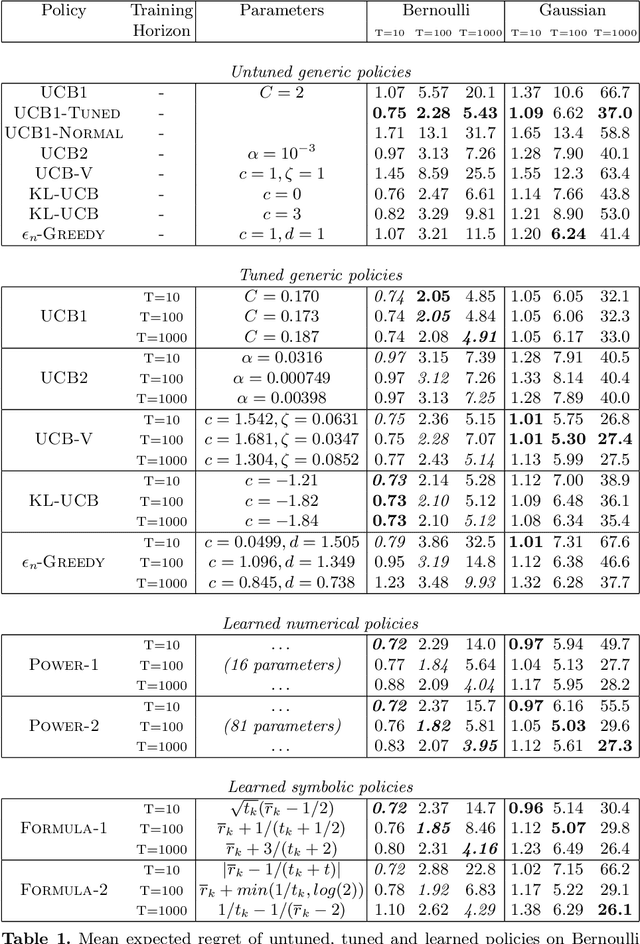
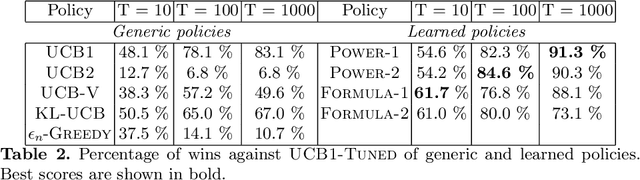
The exploration/exploitation (E/E) dilemma arises naturally in many subfields of Science. Multi-armed bandit problems formalize this dilemma in its canonical form. Most current research in this field focuses on generic solutions that can be applied to a wide range of problems. However, in practice, it is often the case that a form of prior information is available about the specific class of target problems. Prior knowledge is rarely used in current solutions due to the lack of a systematic approach to incorporate it into the E/E strategy. To address a specific class of E/E problems, we propose to proceed in three steps: (i) model prior knowledge in the form of a probability distribution over the target class of E/E problems; (ii) choose a large hypothesis space of candidate E/E strategies; and (iii), solve an optimization problem to find a candidate E/E strategy of maximal average performance over a sample of problems drawn from the prior distribution. We illustrate this meta-learning approach with two different hypothesis spaces: one where E/E strategies are numerically parameterized and another where E/E strategies are represented as small symbolic formulas. We propose appropriate optimization algorithms for both cases. Our experiments, with two-armed Bernoulli bandit problems and various playing budgets, show that the meta-learnt E/E strategies outperform generic strategies of the literature (UCB1, UCB1-Tuned, UCB-v, KL-UCB and epsilon greedy); they also evaluate the robustness of the learnt E/E strategies, by tests carried out on arms whose rewards follow a truncated Gaussian distribution.