Deep Reinforcement Learning for a Two-Echelon Supply Chain with Seasonal Demand

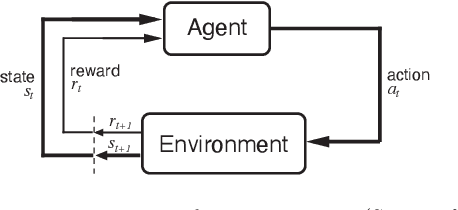
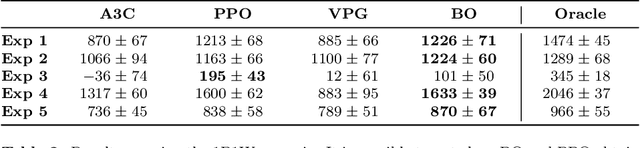
This paper leverages recent developments in reinforcement learning and deep learning to solve the supply chain inventory management problem, a complex sequential decision-making problem consisting of determining the optimal quantity of products to produce and ship to different warehouses over a given time horizon. A mathematical formulation of the stochastic two-echelon supply chain environment is given, which allows an arbitrary number of warehouses and product types to be managed. Additionally, an open-source library that interfaces with deep reinforcement learning algorithms is developed and made publicly available for solving the inventory management problem. Performances achieved by state-of-the-art deep reinforcement learning algorithms are compared through a rich set of numerical experiments on synthetically generated data. The experimental plan is designed and performed, including different structures, topologies, demands, capacities, and costs of the supply chain. Results show that the PPO algorithm adapts very well to different characteristics of the environment. The VPG algorithm almost always converges to a local maximum, even if it typically achieves an acceptable performance level. Finally, A3C is the fastest algorithm, but just like the VPG, it never achieves the best performance when compared to PPO. In conclusion, numerical experiments show that deep reinforcement learning performs consistently better than standard inventory management strategies, such as the static (s, Q)-policy. Thus, it can be considered a practical and effective option for solving real-world instances of the stochastic two-echelon supply chain problem.

Hard and Soft EM in Bayesian Network Learning from Incomplete Data

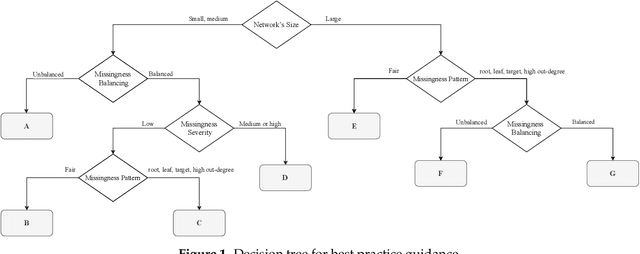
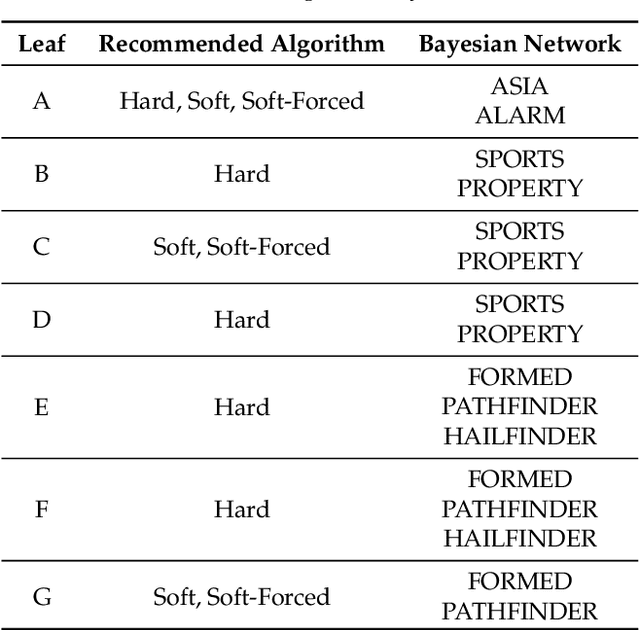
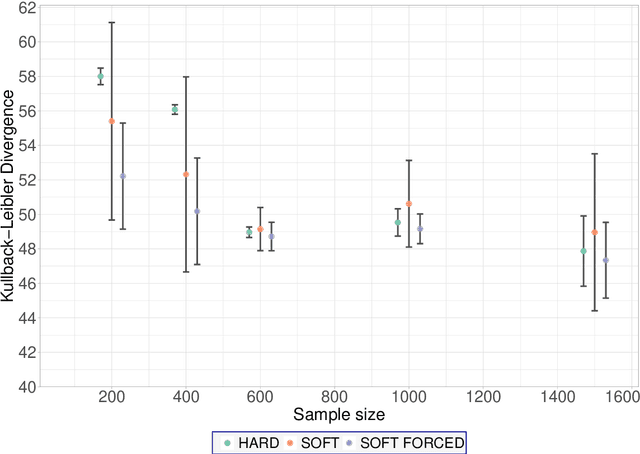
Incomplete data are a common feature in many domains, from clinical trials to industrial applications. Bayesian networks (BNs) are often used in these domains because of their graphical and causal interpretations. BN parameter learning from incomplete data is usually implemented with the Expectation-Maximisation algorithm (EM), which computes the relevant sufficient statistics ("soft EM") using belief propagation. Similarly, the Structural Expectation-Maximisation algorithm (Structural EM) learns the network structure of the BN from those sufficient statistics using algorithms designed for complete data. However, practical implementations of parameter and structure learning often impute missing data ("hard EM") to compute sufficient statistics instead of using belief propagation, for both ease of implementation and computational speed. In this paper, we investigate the question: what is the impact of using imputation instead of belief propagation on the quality of the resulting BNs? From a simulation study using synthetic data and reference BNs, we find that it is possible to recommend one approach over the other in several scenarios based on the characteristics of the data. We then use this information to build a simple decision tree to guide practitioners in choosing the EM algorithm best suited to their problem.