$μ$PC: Scaling Predictive Coding to 100+ Layer Networks

The biological implausibility of backpropagation (BP) has motivated many alternative, brain-inspired algorithms that attempt to rely only on local information, such as predictive coding (PC) and equilibrium propagation. However, these algorithms have notoriously struggled to train very deep networks, preventing them from competing with BP in large-scale settings. Indeed, scaling PC networks (PCNs) has recently been posed as a challenge for the community (Pinchetti et al., 2024). Here, we show that 100+ layer PCNs can be trained reliably using a Depth-$\mu$P parameterisation (Yang et al., 2023; Bordelon et al., 2023) which we call "$\mu$PC". Through an extensive analysis of the scaling behaviour of PCNs, we reveal several pathologies that make standard PCNs difficult to train at large depths. We then show that, despite addressing only some of these instabilities, $\mu$PC allows stable training of very deep (up to 128-layer) residual networks on simple classification tasks with competitive performance and little tuning compared to current benchmarks. Moreover, $\mu$PC enables zero-shot transfer of both weight and activity learning rates across widths and depths. Our results have implications for other local algorithms and could be extended to convolutional and transformer architectures. Code for $\mu$PC is made available as part of a JAX library for PCNs at https://github.com/thebuckleylab/jpc (Innocenti et al., 2024).

JPC: Flexible Inference for Predictive Coding Networks in JAX

We introduce JPC, a JAX library for training neural networks with Predictive Coding. JPC provides a simple, fast and flexible interface to train a variety of PC networks (PCNs) including discriminative, generative and hybrid models. Unlike existing libraries, JPC leverages ordinary differential equation solvers to integrate the gradient flow inference dynamics of PCNs. We find that a second-order solver achieves significantly faster runtimes compared to standard Euler integration, with comparable performance on a range of tasks and network depths. JPC also provides some theoretical tools that can be used to study PCNs. We hope that JPC will facilitate future research of PC. The code is available at https://github.com/thebuckleylab/jpc.

Only Strict Saddles in the Energy Landscape of Predictive Coding Networks?

Predictive coding (PC) is an energy-based learning algorithm that performs iterative inference over network activities before weight updates. Recent work suggests that PC can converge in fewer learning steps than backpropagation thanks to its inference procedure. However, these advantages are not always observed, and the impact of PC inference on learning is theoretically not well understood. Here, we study the geometry of the PC energy landscape at the (inference) equilibrium of the network activities. For deep linear networks, we first show that the equilibrated energy is simply a rescaled mean squared error loss with a weight-dependent rescaling. We then prove that many highly degenerate (non-strict) saddles of the loss including the origin become much easier to escape (strict) in the equilibrated energy. Our theory is validated by experiments on both linear and non-linear networks. Based on these results, we conjecture that all the saddles of the equilibrated energy are strict. Overall, this work suggests that PC inference makes the loss landscape more benign and robust to vanishing gradients, while also highlighting the challenge of speeding up PC inference on large-scale models.

Understanding Predictive Coding as an Adaptive Trust-Region Method

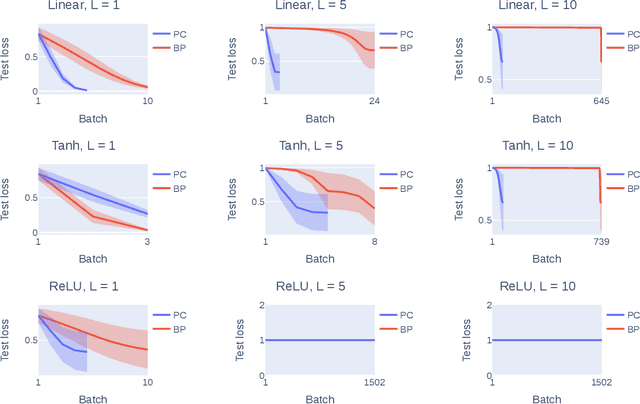
Predictive coding (PC) is a brain-inspired local learning algorithm that has recently been suggested to provide advantages over backpropagation (BP) in biologically relevant scenarios. While theoretical work has mainly focused on showing how PC can approximate BP in various limits, the putative benefits of "natural" PC are less understood. Here we develop a theory of PC as an adaptive trust-region (TR) algorithm that uses second-order information. We show that the learning dynamics of PC can be interpreted as interpolating between BP's loss gradient direction and a TR direction found by the PC inference dynamics. Our theory suggests that PC should escape saddle points faster than BP, a prediction which we prove in a shallow linear model and support with experiments on deeper networks. This work lays a foundation for understanding PC in deep and wide networks.