Word-length entropies and correlations of natural language written texts

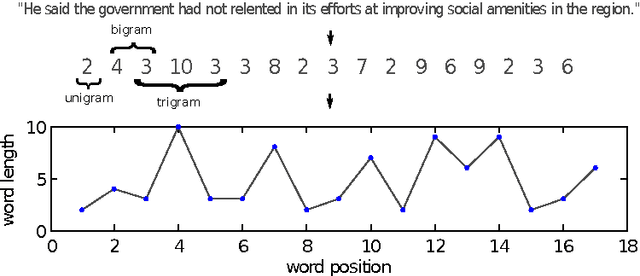
We study the frequency distributions and correlations of the word lengths of ten European languages. Our findings indicate that a) the word-length distribution of short words quantified by the mean value and the entropy distinguishes the Uralic (Finnish) corpus from the others, b) the tails at long words, manifested in the high-order moments of the distributions, differentiate the Germanic languages (except for English) from the Romanic languages and Greek and c) the correlations between nearby word lengths measured by the comparison of the real entropies with those of the shuffled texts are found to be smaller in the case of Germanic and Finnish languages.

Entropy analysis of word-length series of natural language texts: Effects of text language and genre

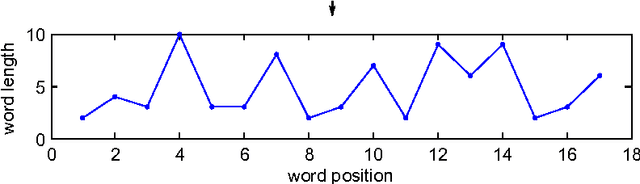
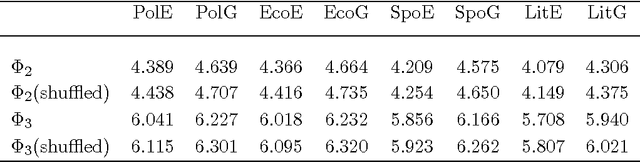
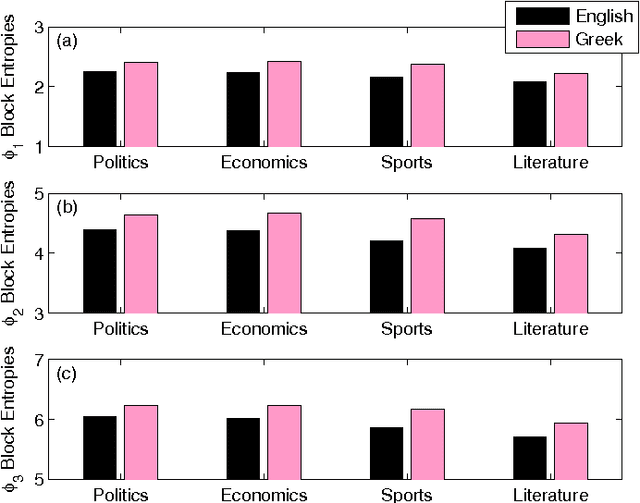
We estimate the $n$-gram entropies of natural language texts in word-length representation and find that these are sensitive to text language and genre. We attribute this sensitivity to changes in the probability distribution of the lengths of single words and emphasize the crucial role of the uniformity of probabilities of having words with length between five and ten. Furthermore, comparison with the entropies of shuffled data reveals the impact of word length correlations on the estimated $n$-gram entropies.