Florin Constantin
Learning Valuation Functions
Sep 02, 2011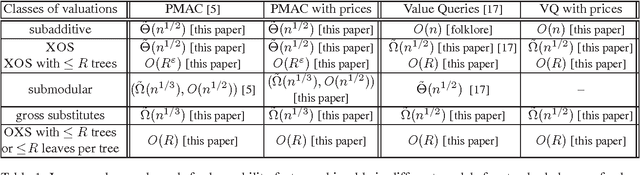
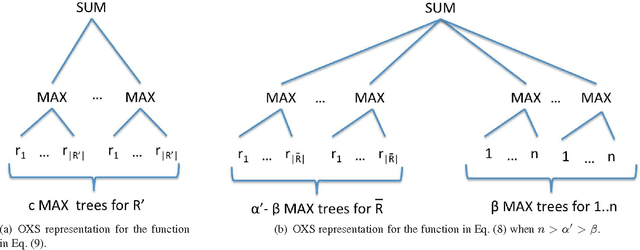
Abstract:In this paper we study the approximate learnability of valuations commonly used throughout economics and game theory for the quantitative encoding of agent preferences. We provide upper and lower bounds regarding the learnability of important subclasses of valuation functions that express no-complementarities. Our main results concern their approximate learnability in the distributional learning (PAC-style) setting. We provide nearly tight lower and upper bounds of $\tilde{\Theta}(n^{1/2})$ on the approximation factor for learning XOS and subadditive valuations, both widely studied superclasses of submodular valuations. Interestingly, we show that the $\tilde{\Omega}(n^{1/2})$ lower bound can be circumvented for XOS functions of polynomial complexity; we provide an algorithm for learning the class of XOS valuations with a representation of polynomial size achieving an $O(n^{\eps})$ approximation factor in time $O(n^{1/\eps})$ for any $\eps > 0$. This highlights the importance of considering the complexity of the target function for polynomial time learning. We also provide new learning results for interesting subclasses of submodular functions. Our upper bounds for distributional learning leverage novel structural results for all these valuation classes. We show that many of these results provide new learnability results in the Goemans et al. model (SODA 2009) of approximate learning everywhere via value queries. We also introduce a new model that is more realistic in economic settings, in which the learner can set prices and observe purchase decisions at these prices rather than observing the valuation function directly. In this model, most of our upper bounds continue to hold despite the fact that the learner receives less information (both for learning in the distributional setting and with value queries), while our lower bounds naturally extend.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge