ELMTEX: Fine-Tuning Large Language Models for Structured Clinical Information Extraction. A Case Study on Clinical Reports

Europe's healthcare systems require enhanced interoperability and digitalization, driving a demand for innovative solutions to process legacy clinical data. This paper presents the results of our project, which aims to leverage Large Language Models (LLMs) to extract structured information from unstructured clinical reports, focusing on patient history, diagnoses, treatments, and other predefined categories. We developed a workflow with a user interface and evaluated LLMs of varying sizes through prompting strategies and fine-tuning. Our results show that fine-tuned smaller models match or surpass larger counterparts in performance, offering efficiency for resource-limited settings. A new dataset of 60,000 annotated English clinical summaries and 24,000 German translations was validated with automated and manual checks. The evaluations used ROUGE, BERTScore, and entity-level metrics. The work highlights the approach's viability and outlines future improvements.

A Quantitative Symbolic Approach to Individual Human Reasoning

Cognitive theories for reasoning are about understanding how humans come to conclusions from a set of premises. Starting from hypothetical thoughts, we are interested which are the implications behind basic everyday language and how do we reason with them. A widely studied topic is whether cognitive theories can account for typical reasoning tasks and be confirmed by own empirical experiments. This paper takes a different view and we do not propose a theory, but instead take findings from the literature and show how these, formalized as cognitive principles within a logical framework, can establish a quantitative notion of reasoning, which we call plausibility. For this purpose, we employ techniques from non-monotonic reasoning and computer science, namely, a solving paradigm called answer set programming (ASP). Finally, we can fruitfully use plausibility reasoning in ASP to test the effects of an existing experiment and explain different majority responses.

The Model Counting Competition 2020

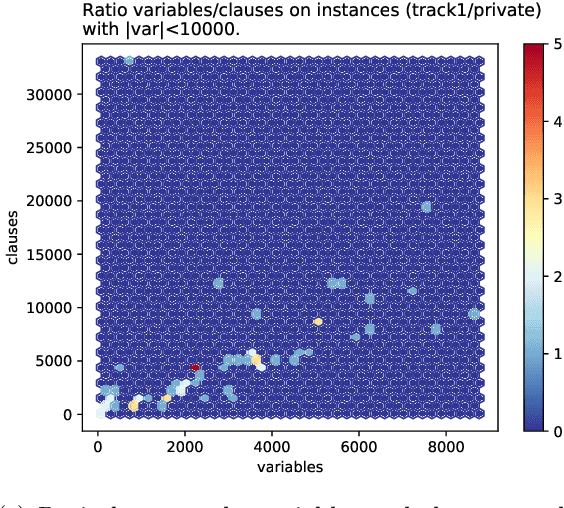
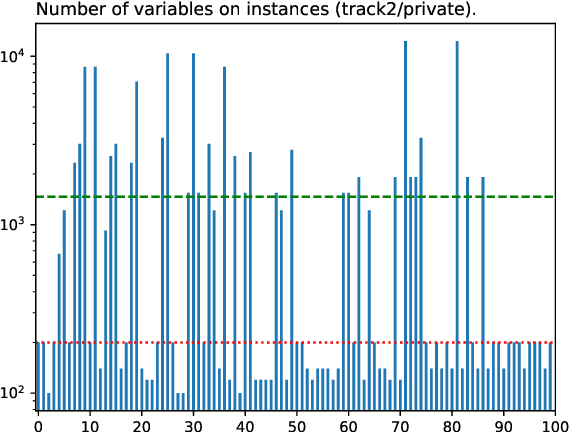
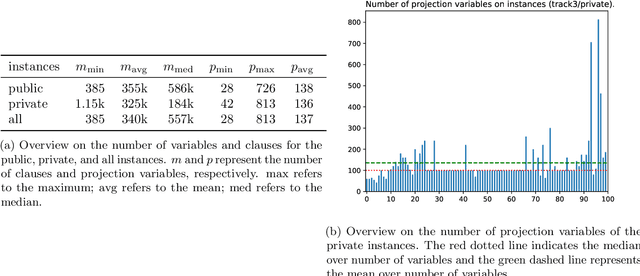
Many computational problems in modern society account to probabilistic reasoning, statistics, and combinatorics. A variety of these real-world questions can be solved by representing the question in (Boolean) formulas and associating the number of models of the formula directly with the answer to the question. Since there has been an increasing interest in practical problem solving for model counting over the last years, the Model Counting (MC) Competition was conceived in fall 2019. The competition aims to foster applications, identify new challenging benchmarks, and to promote new solvers and improve established solvers for the model counting problem and versions thereof. We hope that the results can be a good indicator of the current feasibility of model counting and spark many new applications. In this paper, we report on details of the Model Counting Competition 2020, about carrying out the competition, and the results. The competition encompassed three versions of the model counting problem, which we evaluated in separate tracks. The first track featured the model counting problem (MC), which asks for the number of models of a given Boolean formula. On the second track, we challenged developers to submit programs that solve the weighted model counting problem (WMC). The last track was dedicated to projected model counting (PMC). In total, we received a surprising number of 9 solvers in 34 versions from 8 groups.