Performance analysis of downlink MIMO-NOMA systems over Weibull fading channels

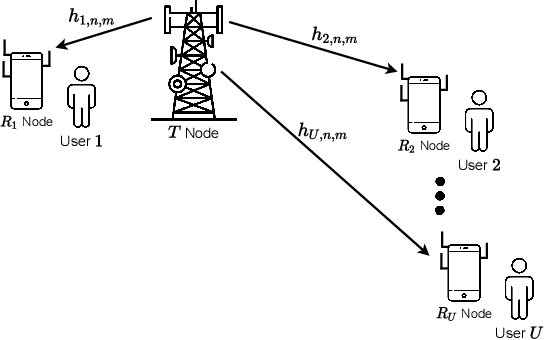
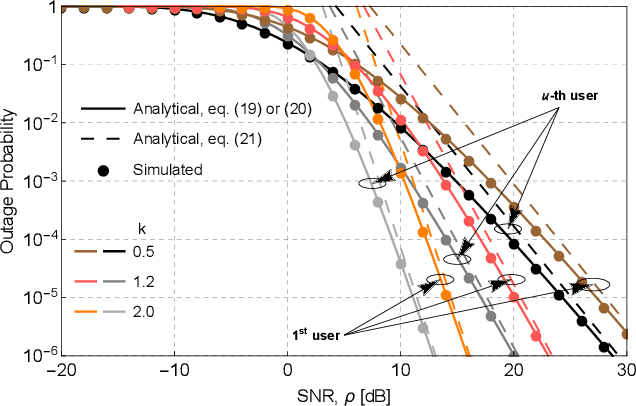
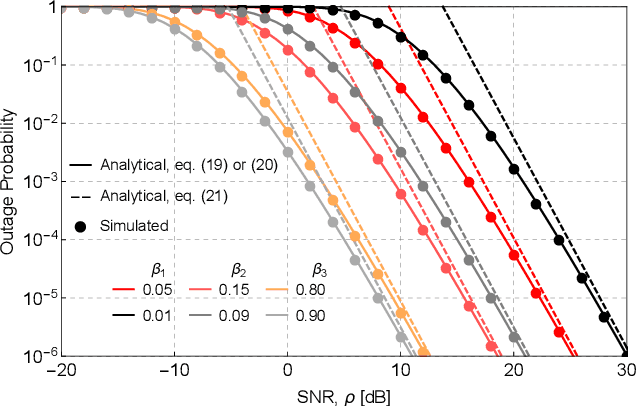
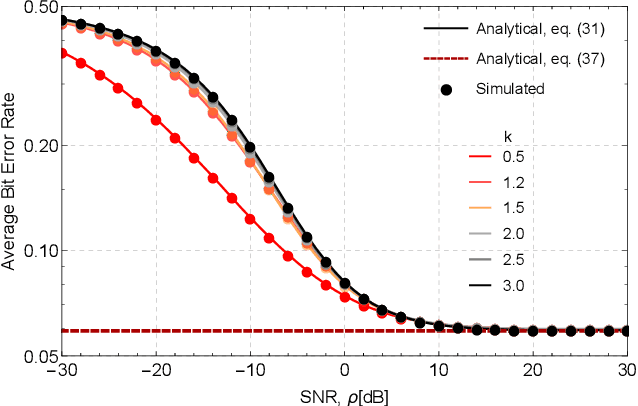
This work analyzes the performance of a downlink multiple-input multiple-output (MIMO) non-orthogonal multiple access (NOMA) multi-user communications system. To reduce hardware complexity and exploit antenna diversity, we consider a transmit antenna selection (TAS) scheme and equal-gain combining (EGC) receivers operating over independent and identically distributed (i.i.d.) Weibull fading channels. Performance metrics such as the outage probability (OP) and the average bit error rate (ABER) are derived in an exact manner. An asymptotic analysis for the OP and for the ABER is also carried out. Moreover, we obtain exact expressions for the probability density function (PDF) and the cumulative distribution function (CDF) of the end-to-end signal-to-noise ratio (SNR). Interestingly, our results indicate that, except for the first user (nearest user), in a high-SNR regime the ABER achieves a performance floor that depends solely on the user's power allocation coefficient and on the type of modulation, and not on the channel statistics or the amount of transmit and receive antennas. To the best of the authors' knowledge, no performance analyses have been reported in the literature for the considered scenario. The validity of all our expressions is confirmed via Monte-Carlo simulations.

Doppler Estimation for High-Velocity Targets Using Subpulse Processing and the Classic Chinese Remainder Theorem

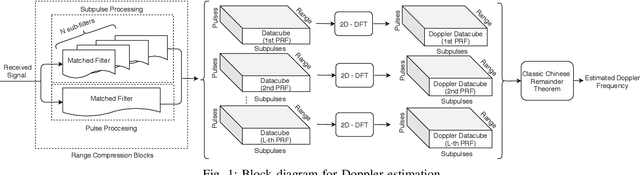
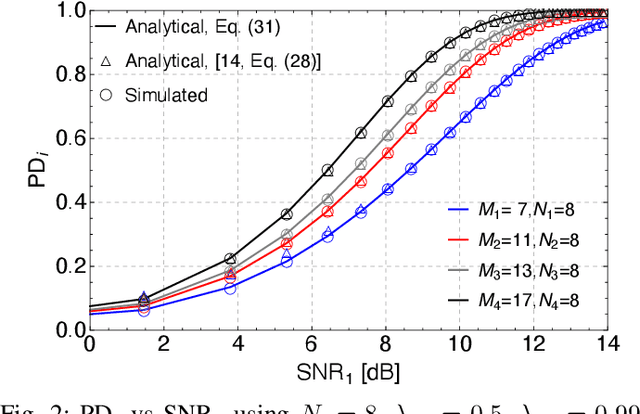
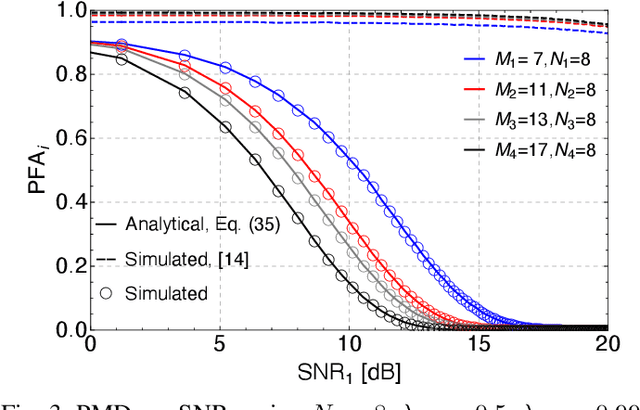
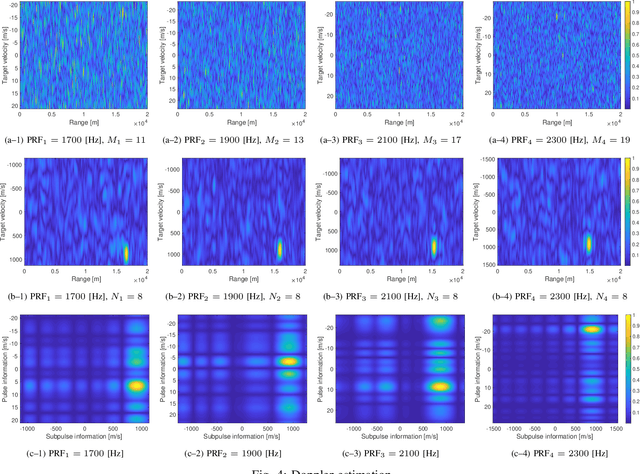
In pulsed Doppler radars, the classic Chinese remainder theorem (CCRT) is a common method to resolve Doppler ambiguities caused by fast-moving targets. Another issue concerning high-velocity targets is related to the loss in the signal-to-noise ratio (SNR) after performing range compression. In particular, this loss can be partially mitigated by the use of subpulse processing (SP). Modern radars combine these techniques in order to reliably unfold the target velocity. However, the presence of background noise may compromise the Doppler estimates. Hence, a rigorous statistical analysis is imperative. In this work, we provide a comprehensive analysis on Doppler estimation. In particular, we derive novel closed-form expressions for the probability of detection (PD) and probability of false alarm (PFA). To this end, we consider the newly introduce SP along with the CCRT. A comparison analysis between SP and the classic pulse processing (PP) technique is also carried out. Numerical results and Monte-Carlo simulations corroborate the validity of our expressions and show that the SP-plus-CCRT technique helps to greatly reduce the PFA compared to previous studies, thereby improving radar detection.

New Findings on GLRT Radar Detection of Nonfluctuating Targets via Phased Arrays

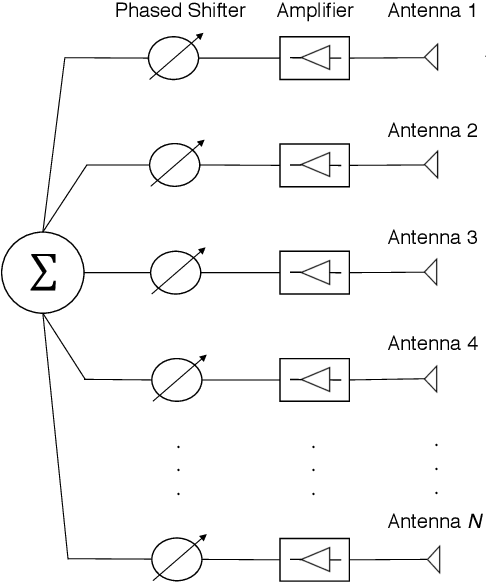
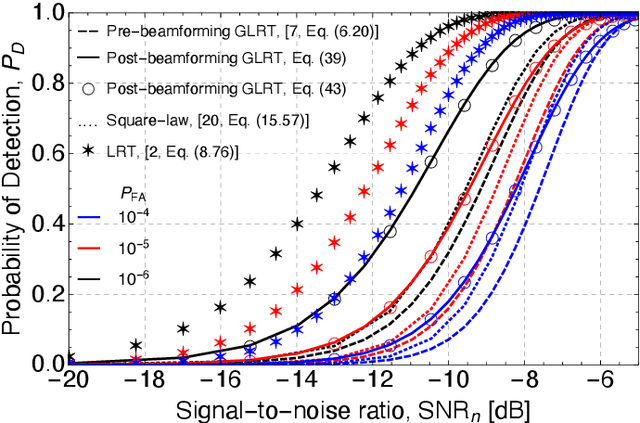
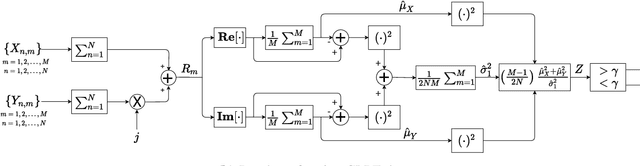
This paper addresses the standard generalized likelihood ratio test (GLRT) detection problem of weak signals in background noise. In so doing, we consider a nonfluctuating target embedded in complex white Gaussian noise (CWGN), in which the amplitude of the target echo and the noise power are assumed to be unknown. Important works have analyzed the performance for the referred scenario and proposed GLRT-based detectors. Such detectors are projected at an early stage (i.e., prior to the formation of a post-beamforming scalar waveform), thereby imposing high demands on hardware, processing, and data storage. From a hardware perspective, most radar systems fail to meet these strong requirements. In fact, due to hardware and computational constraints, most radars use a combination of analog and digital beamformers (sums) before any estimation or further pre-processing. The rationale behind this study is to derive a GLRT detector that meets the hardware and system requirements. In this work, we design and analyze a more practical and easy-to-implement GLRT detector, which is projected after the analog beamforming. The performance of the proposed detector is analyzed and the probabilities of detection (PD) and false alarm (PFA) are derived in closed form. Moreover, we show that in the low signal-to-noise ratio (SNR) regime, the post-beamforming GLRT detector performs better than both the classic pre-beamforming GLRT detector and the square-law detector. This finding suggests that if the signals are weak, instead of processing the signals separately, we first must to reinforce the overall signal and then assembling the system's detection statistic. At last, the SNR losses are quantified, in which the superiority of the post-beamforming GLRT detector was evidenced as the number of antennas and samples increase.