Doppler Estimation for High-Velocity Targets Using Subpulse Processing and the Classic Chinese Remainder Theorem
Paper and Code
Jan 27, 2021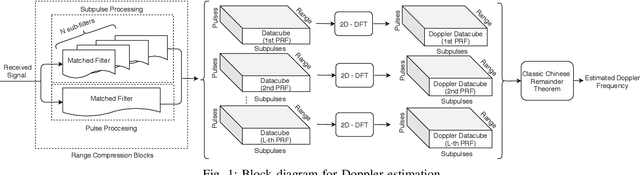
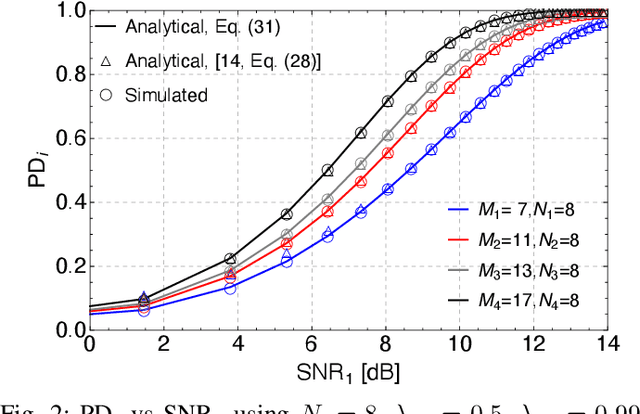
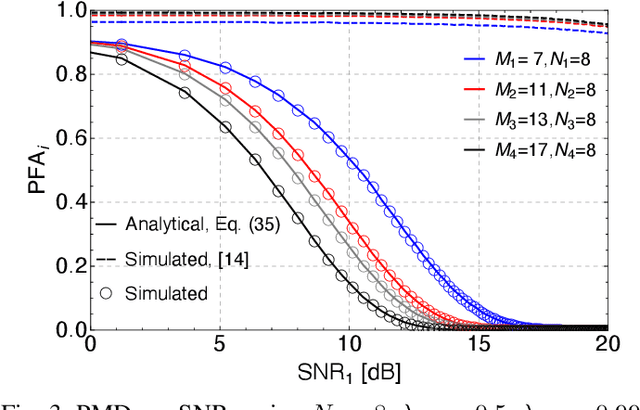
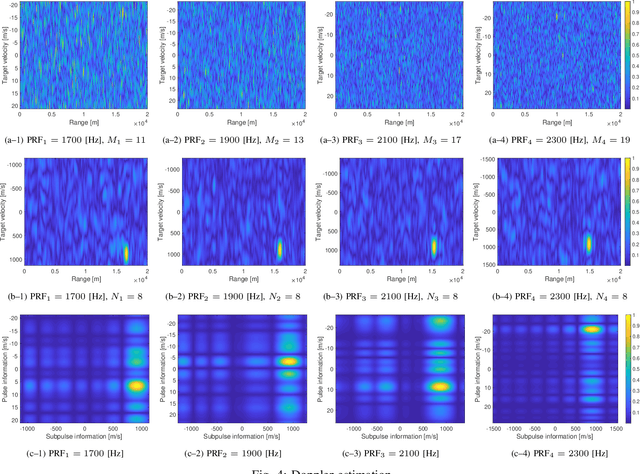
In pulsed Doppler radars, the classic Chinese remainder theorem (CCRT) is a common method to resolve Doppler ambiguities caused by fast-moving targets. Another issue concerning high-velocity targets is related to the loss in the signal-to-noise ratio (SNR) after performing range compression. In particular, this loss can be partially mitigated by the use of subpulse processing (SP). Modern radars combine these techniques in order to reliably unfold the target velocity. However, the presence of background noise may compromise the Doppler estimates. Hence, a rigorous statistical analysis is imperative. In this work, we provide a comprehensive analysis on Doppler estimation. In particular, we derive novel closed-form expressions for the probability of detection (PD) and probability of false alarm (PFA). To this end, we consider the newly introduce SP along with the CCRT. A comparison analysis between SP and the classic pulse processing (PP) technique is also carried out. Numerical results and Monte-Carlo simulations corroborate the validity of our expressions and show that the SP-plus-CCRT technique helps to greatly reduce the PFA compared to previous studies, thereby improving radar detection.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge