Marco Antonio Miguel Miranda
New Findings on GLRT Radar Detection of Nonfluctuating Targets via Phased Arrays
Jan 26, 2021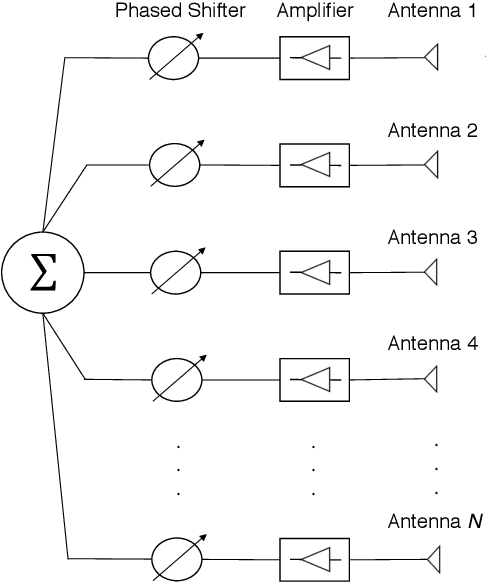
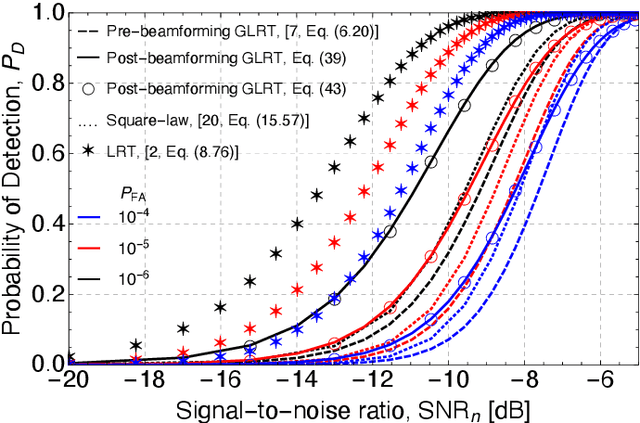
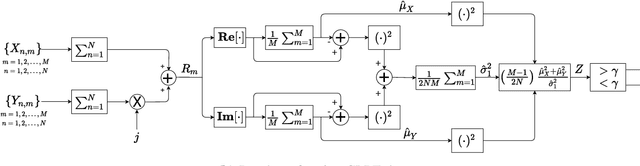
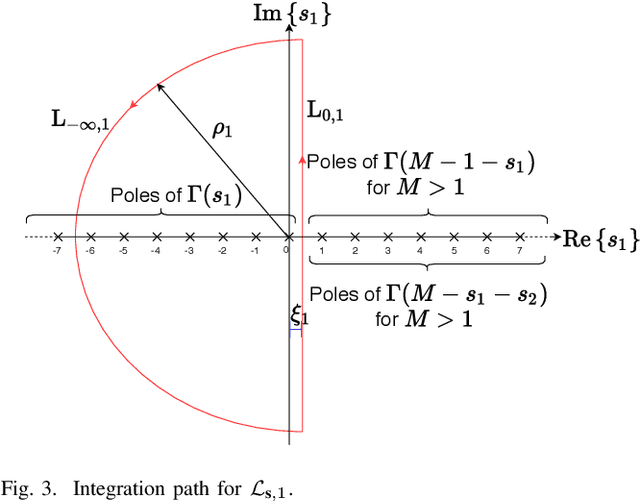
Abstract:This paper addresses the standard generalized likelihood ratio test (GLRT) detection problem of weak signals in background noise. In so doing, we consider a nonfluctuating target embedded in complex white Gaussian noise (CWGN), in which the amplitude of the target echo and the noise power are assumed to be unknown. Important works have analyzed the performance for the referred scenario and proposed GLRT-based detectors. Such detectors are projected at an early stage (i.e., prior to the formation of a post-beamforming scalar waveform), thereby imposing high demands on hardware, processing, and data storage. From a hardware perspective, most radar systems fail to meet these strong requirements. In fact, due to hardware and computational constraints, most radars use a combination of analog and digital beamformers (sums) before any estimation or further pre-processing. The rationale behind this study is to derive a GLRT detector that meets the hardware and system requirements. In this work, we design and analyze a more practical and easy-to-implement GLRT detector, which is projected after the analog beamforming. The performance of the proposed detector is analyzed and the probabilities of detection (PD) and false alarm (PFA) are derived in closed form. Moreover, we show that in the low signal-to-noise ratio (SNR) regime, the post-beamforming GLRT detector performs better than both the classic pre-beamforming GLRT detector and the square-law detector. This finding suggests that if the signals are weak, instead of processing the signals separately, we first must to reinforce the overall signal and then assembling the system's detection statistic. At last, the SNR losses are quantified, in which the superiority of the post-beamforming GLRT detector was evidenced as the number of antennas and samples increase.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge