Farshad Lahouti
How to Query An Oracle? Efficient Strategies to Label Data
Oct 05, 2021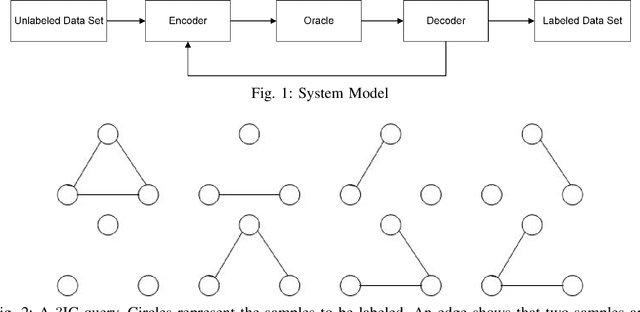
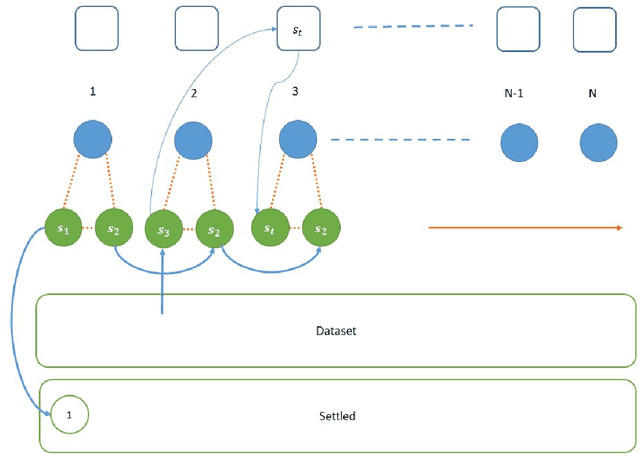
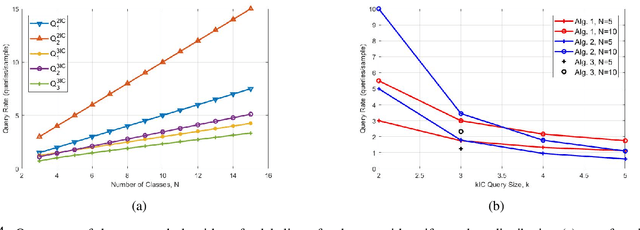
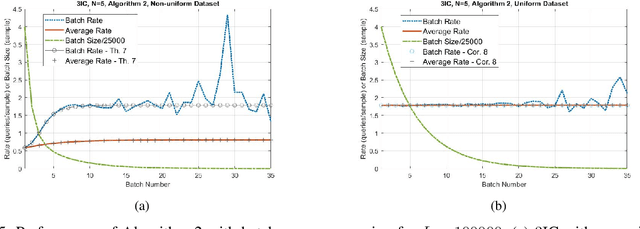
Abstract:We consider the basic problem of querying an expert oracle for labeling a dataset in machine learning. This is typically an expensive and time consuming process and therefore, we seek ways to do so efficiently. The conventional approach involves comparing each sample with (the representative of) each class to find a match. In a setting with $N$ equally likely classes, this involves $N/2$ pairwise comparisons (queries per sample) on average. We consider a $k$-ary query scheme with $k\ge 2$ samples in a query that identifies (dis)similar items in the set while effectively exploiting the associated transitive relations. We present a randomized batch algorithm that operates on a round-by-round basis to label the samples and achieves a query rate of $O(\frac{N}{k^2})$. In addition, we present an adaptive greedy query scheme, which achieves an average rate of $\approx 0.2N$ queries per sample with triplet queries. For the proposed algorithms, we investigate the query rate performance analytically and with simulations. Empirical studies suggest that each triplet query takes an expert at most 50\% more time compared with a pairwise query, indicating the effectiveness of the proposed $k$-ary query schemes. We generalize the analyses to nonuniform class distributions when possible.
Distributed Solution of Large-Scale Linear Systems via Accelerated Projection-Based Consensus
Dec 11, 2017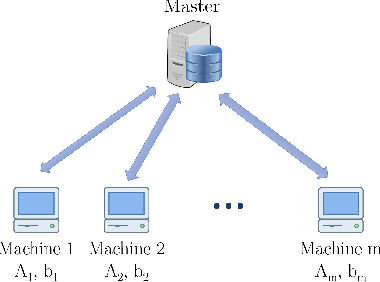

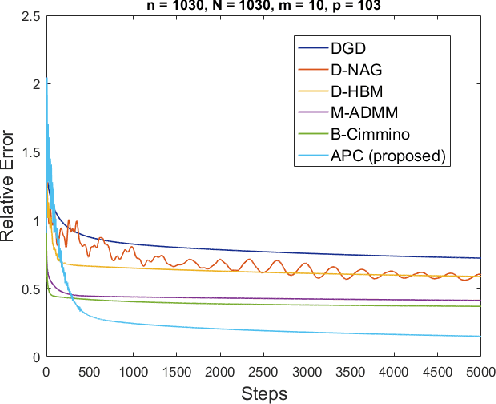
Abstract:Solving a large-scale system of linear equations is a key step at the heart of many algorithms in machine learning, scientific computing, and beyond. When the problem dimension is large, computational and/or memory constraints make it desirable, or even necessary, to perform the task in a distributed fashion. In this paper, we consider a common scenario in which a taskmaster intends to solve a large-scale system of linear equations by distributing subsets of the equations among a number of computing machines/cores. We propose an accelerated distributed consensus algorithm, in which at each iteration every machine updates its solution by adding a scaled version of the projection of an error signal onto the nullspace of its system of equations, and where the taskmaster conducts an averaging over the solutions with momentum. The convergence behavior of the proposed algorithm is analyzed in detail and analytically shown to compare favorably with the convergence rate of alternative distributed methods, namely distributed gradient descent, distributed versions of Nesterov's accelerated gradient descent and heavy-ball method, the block Cimmino method, and ADMM. On randomly chosen linear systems, as well as on real-world data sets, the proposed method offers significant speed-up relative to all the aforementioned methods. Finally, our analysis suggests a novel variation of the distributed heavy-ball method, which employs a particular distributed preconditioning, and which achieves the same theoretical convergence rate as the proposed consensus-based method.
Fundamental Limits of Budget-Fidelity Trade-off in Label Crowdsourcing
Aug 25, 2016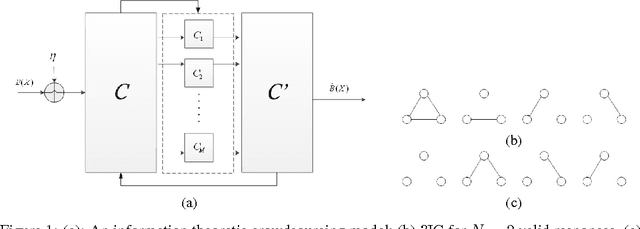

Abstract:Digital crowdsourcing (CS) is a modern approach to perform certain large projects using small contributions of a large crowd. In CS, a taskmaster typically breaks down the project into small batches of tasks and assigns them to so-called workers with imperfect skill levels. The crowdsourcer then collects and analyzes the results for inference and serving the purpose of the project. In this work, the CS problem, as a human-in-the-loop computation problem, is modeled and analyzed in an information theoretic rate-distortion framework. The purpose is to identify the ultimate fidelity that one can achieve by any form of query from the crowd and any decoding (inference) algorithm with a given budget. The results are established by a joint source channel (de)coding scheme, which represent the query scheme and inference, over parallel noisy channels, which model workers with imperfect skill levels. We also present and analyze a query scheme dubbed $k$-ary incidence coding and study optimized query pricing in this setting.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge