How to Query An Oracle? Efficient Strategies to Label Data
Paper and Code
Oct 05, 2021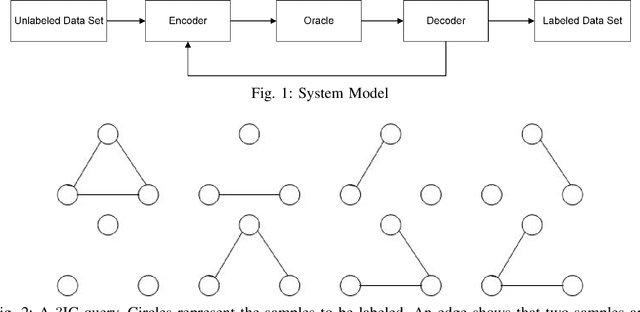
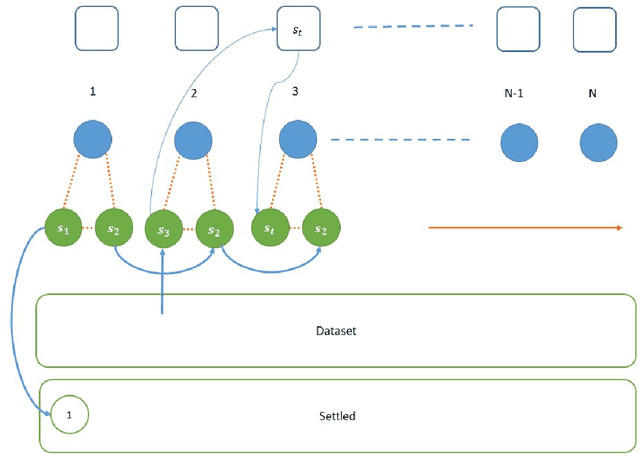
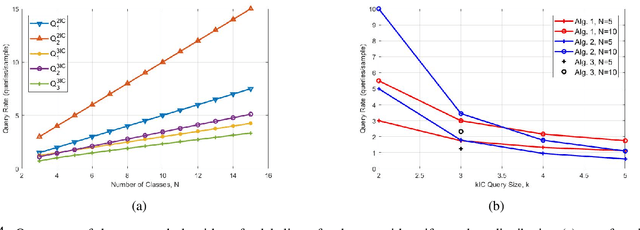
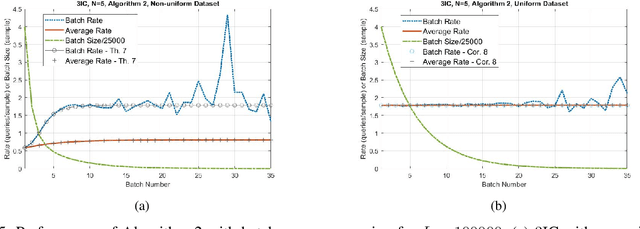
We consider the basic problem of querying an expert oracle for labeling a dataset in machine learning. This is typically an expensive and time consuming process and therefore, we seek ways to do so efficiently. The conventional approach involves comparing each sample with (the representative of) each class to find a match. In a setting with $N$ equally likely classes, this involves $N/2$ pairwise comparisons (queries per sample) on average. We consider a $k$-ary query scheme with $k\ge 2$ samples in a query that identifies (dis)similar items in the set while effectively exploiting the associated transitive relations. We present a randomized batch algorithm that operates on a round-by-round basis to label the samples and achieves a query rate of $O(\frac{N}{k^2})$. In addition, we present an adaptive greedy query scheme, which achieves an average rate of $\approx 0.2N$ queries per sample with triplet queries. For the proposed algorithms, we investigate the query rate performance analytically and with simulations. Empirical studies suggest that each triplet query takes an expert at most 50\% more time compared with a pairwise query, indicating the effectiveness of the proposed $k$-ary query schemes. We generalize the analyses to nonuniform class distributions when possible.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge