Reactive Answer Set Programming

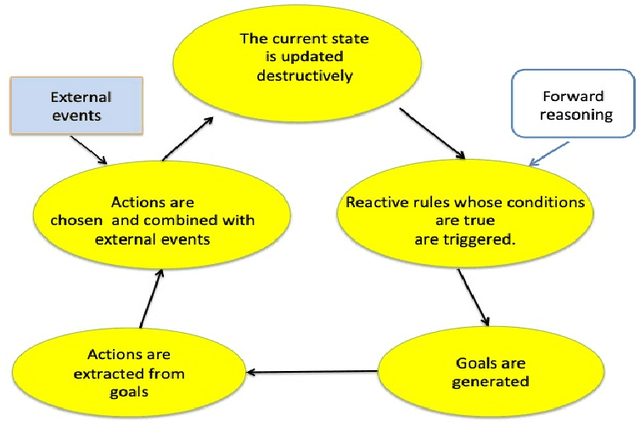
Logic Production System (LPS) is a logic-based framework for modelling reactive behaviour. Based on abductive logic programming, it combines reactive rules with logic programs, a database and a causal theory that specifies transitions between the states of the database. This paper proposes a systematic mapping of the Kernel of this framework (called KELPS) into an answer set program (ASP). For this purpose a new variant of KELPS with finite models, called $n$-distance KELPS, is introduced. A formal definition of the mapping from this $n$-distance KELPS to ASP is given and proven sound and complete. The Answer Set Programming paradigm allows to capture additional behaviours to the basic reactivity of KELPS, in particular proactive, preemptive and prospective behaviours. These are all discussed and illustrated with examples. Then a hybrid framework is proposed that integrates KELPS and ASP, allowing to combine the strengths of both paradigms. Under consideration in Theory and Practice of Logic Programming (TPLP).

Programming in logic without logic programming

In previous work, we proposed a logic-based framework in which computation is the execution of actions in an attempt to make reactive rules of the form if antecedent then consequent true in a canonical model of a logic program determined by an initial state, sequence of events, and the resulting sequence of subsequent states. In this model-theoretic semantics, reactive rules are the driving force, and logic programs play only a supporting role. In the canonical model, states, actions and other events are represented with timestamps. But in the operational semantics, for the sake of efficiency, timestamps are omitted and only the current state is maintained. State transitions are performed reactively by executing actions to make the consequents of rules true whenever the antecedents become true. This operational semantics is sound, but incomplete. It cannot make reactive rules true by preventing their antecedents from becoming true, or by proactively making their consequents true before their antecedents become true. In this paper, we characterize the notion of reactive model, and prove that the operational semantics can generate all and only such models. In order to focus on the main issues, we omit the logic programming component of the framework.

Towards a Logic-Based Unifying Framework for Computing

In this paper we propose a logic-based, framework inspired by artificial intelligence, but scaled down for practical database and programming applications. Computation in the framework is viewed as the task of generating a sequence of state transitions, with the purpose of making an agent's goals all true. States are represented by sets of atomic sentences (or facts), representing the values of program variables, tuples in a coordination language, facts in relational databases, or Herbrand models. In the model-theoretic semantics, the entire sequence of states and events are combined into a single model-theoretic structure, by associating timestamps with facts and events. But in the operational semantics, facts are updated destructively, without timestamps. We show that the model generated by destructive updates is identical to the model generated by reasoning with facts containing timestamps. We also extend the model with intentional predicates and composite event predicates defined by logic programs containing conditions in first-order logic, which query the current state.

Computational Logic Foundations of KGP Agents

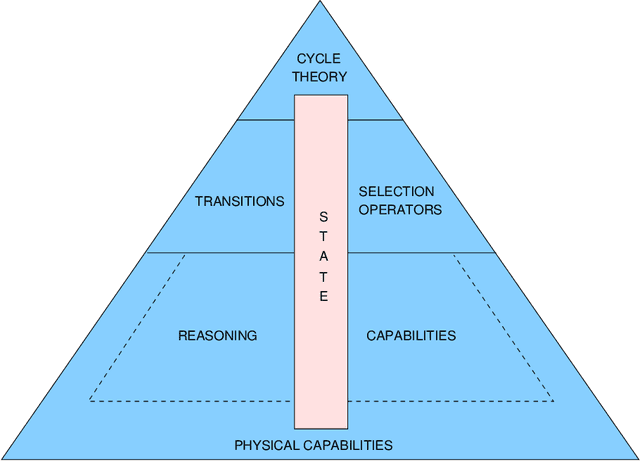
This paper presents the computational logic foundations of a model of agency called the KGP (Knowledge, Goals and Plan model. This model allows the specification of heterogeneous agents that can interact with each other, and can exhibit both proactive and reactive behaviour allowing them to function in dynamic environments by adjusting their goals and plans when changes happen in such environments. KGP provides a highly modular agent architecture that integrates a collection of reasoning and physical capabilities, synthesised within transitions that update the agents state in response to reasoning, sensing and acting. Transitions are orchestrated by cycle theories that specify the order in which transitions are executed while taking into account the dynamic context and agent preferences, as well as selection operators for providing inputs to transitions.