Destination-Constrained Linear Dynamical System Modeling in Set-Valued Frameworks

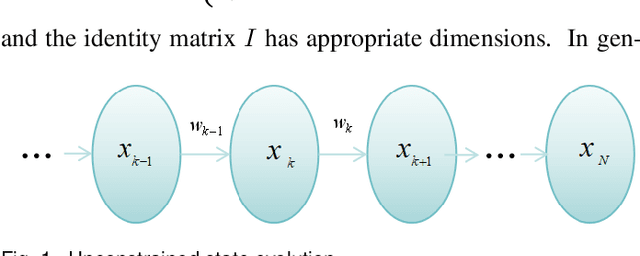
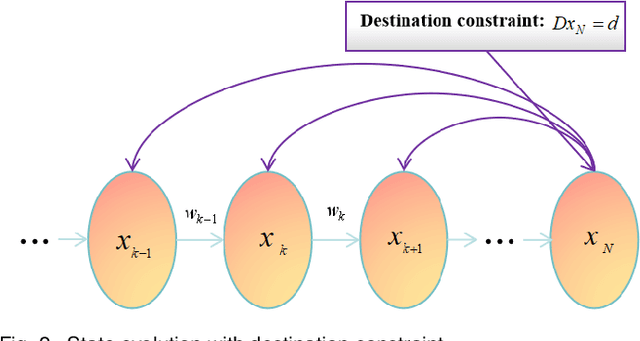
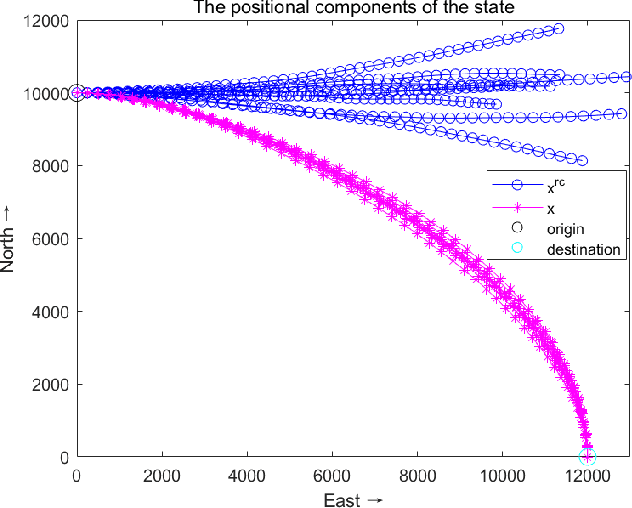
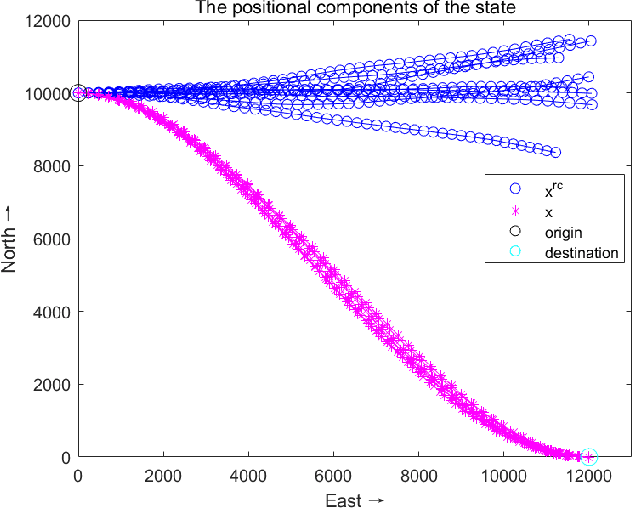
Directional motion towards a specified destination is a common occurrence in physical processes and human societal activities. Utilizing this prior information can significantly improve the control and predictive performance of system models. This paper primarily focuses on reconstructing linear dynamic system models based on destination constraints in the set-valued framework. We treat destination constraints as inherent information in the state evolution process and employ convex optimization techniques to construct a coherent and robust state model. This refined model effectively captures the impact of destination constraints on the state evolution at each time step. Furthermore, we design an optimal weight matrix for the reconstructed model to ensure smoother and more natural trajectories of state evolution. We also analyze the theoretical guarantee of optimality for this weight matrix and the properties of the reconstructed model. Finally, simulation experiments verify that the reconstructed model has significant advantages over the unconstrained and unoptimized weighted models and constrains the evolution of state trajectories with different starting and ending points.

Seamless Tracking of Group Targets and Ungrouped Targets Using Belief Propagation

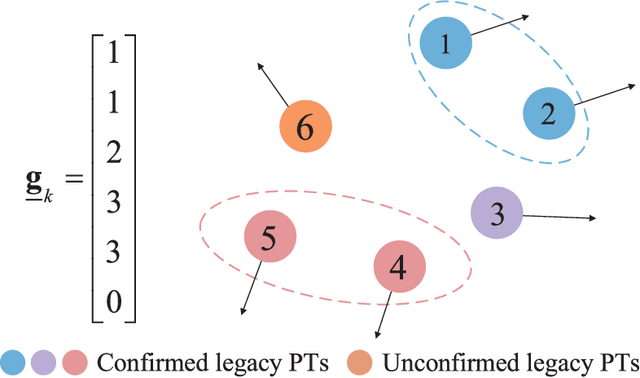
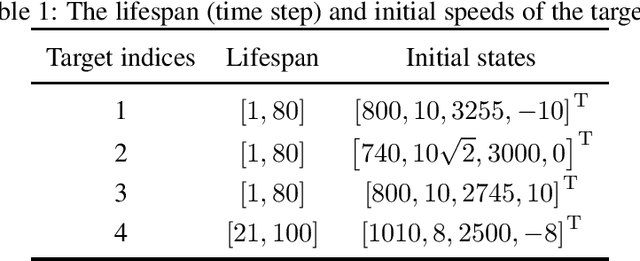
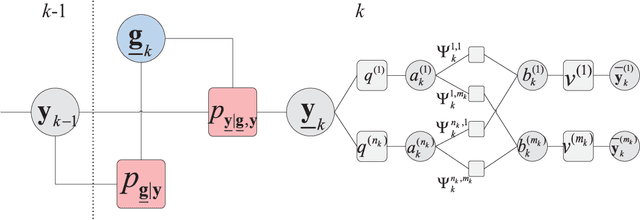
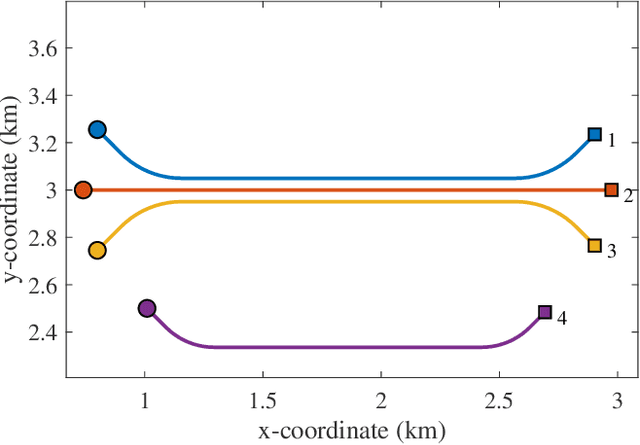
This paper considers the problem of tracking a large-scale number of group targets. Usually, multi-target in most tracking scenarios are assumed to have independent motion and are well-separated. However, for group target tracking (GTT), the targets within groups are closely spaced and move in a coordinated manner, the groups can split or merge, and the numbers of targets in groups may be large, which lead to more challenging data association, filtering and computation problems. Within the belief propagation (BP) framework, we propose a scalable group target belief propagation (GTBP) method by jointly inferring target existence variables, group structure, data association and target states. The method can efficiently calculate the approximations of the marginal posterior distributions of these variables by performing belief propagation on the devised factor graph. As a consequence, GTBP is capable of capturing the changes in group structure, e.g., group splitting and merging. Furthermore, we model the evolution of targets as the co-action of the group or single-target motions specified by the possible group structures and corresponding probabilities. This flexible modeling enables seamless and simultaneous tracking of multiple group targets and ungrouped targets. Particularly, GTBP has excellent scalability and low computational complexity. It not only maintains the same scalability as BP, i.e., scaling linearly in the number of sensor measurements and quadratically in the number of targets, but also only scales linearly in the number of preserved group partitions. Finally, numerical experiments are presented to demonstrate the effectiveness and scalability of the proposed GTBP method.