Destination-Constrained Linear Dynamical System Modeling in Set-Valued Frameworks
Paper and Code
Mar 26, 2024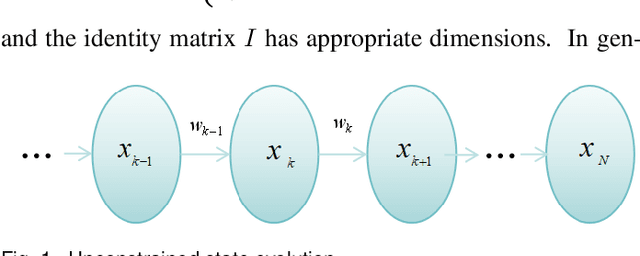
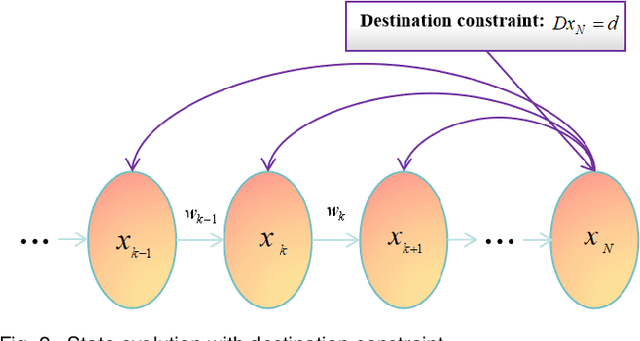
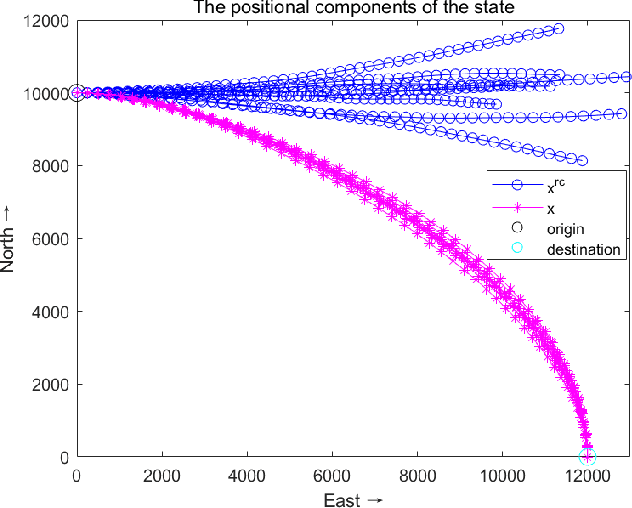
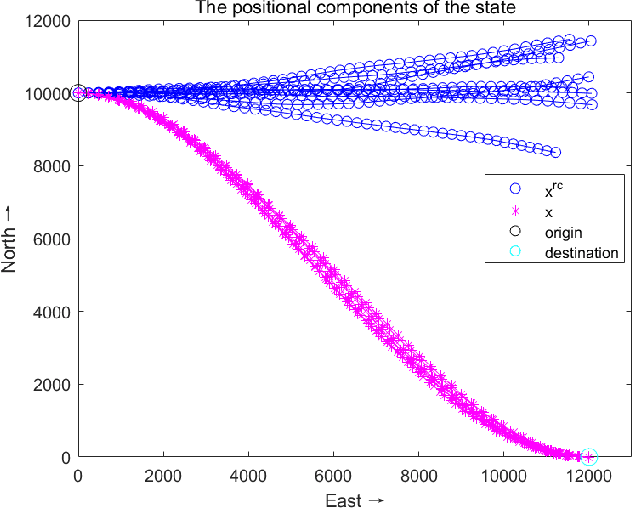
Directional motion towards a specified destination is a common occurrence in physical processes and human societal activities. Utilizing this prior information can significantly improve the control and predictive performance of system models. This paper primarily focuses on reconstructing linear dynamic system models based on destination constraints in the set-valued framework. We treat destination constraints as inherent information in the state evolution process and employ convex optimization techniques to construct a coherent and robust state model. This refined model effectively captures the impact of destination constraints on the state evolution at each time step. Furthermore, we design an optimal weight matrix for the reconstructed model to ensure smoother and more natural trajectories of state evolution. We also analyze the theoretical guarantee of optimality for this weight matrix and the properties of the reconstructed model. Finally, simulation experiments verify that the reconstructed model has significant advantages over the unconstrained and unoptimized weighted models and constrains the evolution of state trajectories with different starting and ending points.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge