RecSys Challenge 2023: From data preparation to prediction, a simple, efficient, robust and scalable solution

The RecSys Challenge 2023, presented by ShareChat, consists to predict if an user will install an application on his smartphone after having seen advertising impressions in ShareChat & Moj apps. This paper presents the solution of 'Team UMONS' to this challenge, giving accurate results (our best score is 6.622686) with a relatively small model that can be easily implemented in different production configurations. Our solution scales well when increasing the dataset size and can be used with datasets containing missing values.

Bounded Simplex-Structured Matrix Factorization

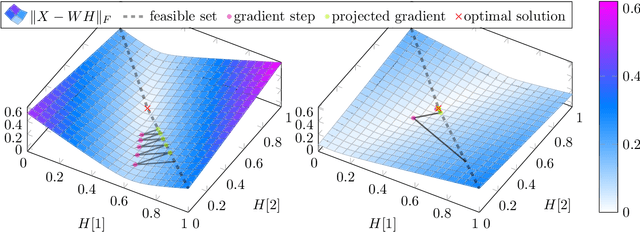
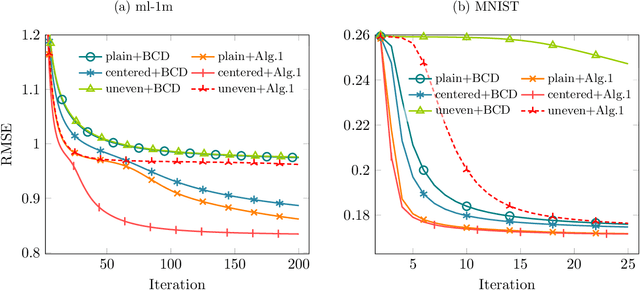
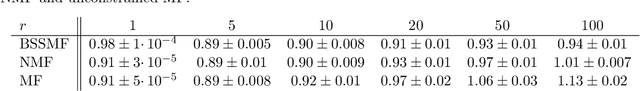
In this paper, we propose a new low-rank matrix factorization model dubbed bounded simplex-structured matrix factorization (BSSMF). Given an input matrix $X$ and a factorization rank $r$, BSSMF looks for a matrix $W$ with $r$ columns and a matrix $H$ with $r$ rows such that $X \approx WH$ where the entries in each column of $W$ are bounded, that is, they belong to given intervals, and the columns of $H$ belong to the probability simplex, that is, $H$ is column stochastic. BSSMF generalizes nonnegative matrix factorization (NMF), and simplex-structured matrix factorization (SSMF). BSSMF is particularly well suited when the entries of the input matrix $X$ belong to a given interval; for example when the rows of $X$ represent images, or $X$ is a rating matrix such as in the Netflix and MovieLens data sets where the entries of $X$ belong to the interval $[1,5]$. The simplex-structured matrix $H$ not only leads to an easily understandable decomposition providing a soft clustering of the columns of $X$, but implies that the entries of each column of $WH$ belong to the same intervals as the columns of $W$. In this paper, we first propose a fast algorithm for BSSMF, even in the presence of missing data in $X$. Then we provide identifiability conditions for BSSMF, that is, we provide conditions under which BSSMF admits a unique decomposition, up to trivial ambiguities. Finally, we illustrate the effectiveness of BSSMF on two applications: extraction of features in a set of images, and the matrix completion problem for recommender systems.

A One-Class Decision Tree Based on Kernel Density Estimation

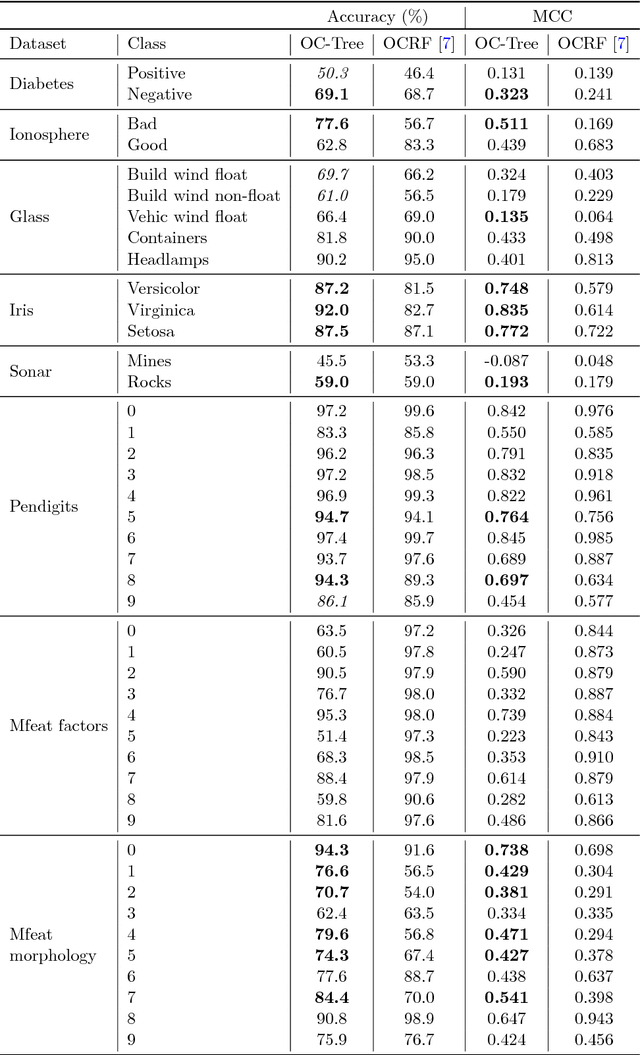
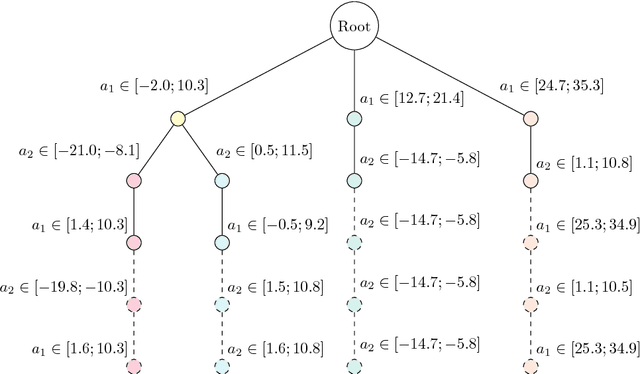
One-Class Classification (OCC) is a domain of machine learning which achieves training by means of a single class sample. The present work aims at developing a one-class model which addresses concerns of both performance and readability. To this end, we propose a hybrid OCC method which relies on density estimation as part of a tree-based learning algorithm. Within a greedy and recursive approach, our proposal rests on kernel density estimation to split a data subset on the basis of one or several intervals of interest. Our method shows favorable performance in comparison with common methods of the literature on a range of benchmark datasets.