Low-Rank Matrix Factorizations with Volume-based Constraints and Regularizations

Low-rank matrix factorizations are a class of linear models widely used in various fields such as machine learning, signal processing, and data analysis. These models approximate a matrix as the product of two smaller matrices, where the left matrix captures latent features while the right matrix linearly decomposes the data based on these features. There are many ways to define what makes a component "important." Standard LRMFs, such as the truncated singular value decomposition, focus on minimizing the distance between the original matrix and its low-rank approximation. In this thesis, the notion of "importance" is closely linked to interpretability and uniqueness, which are key to obtaining reliable and meaningful results. This thesis thus focuses on volume-based constraints and regularizations designed to enhance interpretability and uniqueness. We first introduce two new volume-constrained LRMFs designed to enhance these properties. The first assumes that data points are naturally bounded (e.g., movie ratings between 1 and 5 stars) and can be explained by convex combinations of features within the same bounds, allowing them to be interpreted in the same way as the data. The second model is more general, constraining the factors to belong to convex polytopes. Then, two variants of volume-regularized LRMFs are proposed. The first minimizes the volume of the latent features, encouraging them to cluster closely together, while the second maximizes the volume of the decompositions, promoting sparse representations. Across all these models, uniqueness is achieved under the core principle that the factors must be "sufficiently scattered" within their respective feasible sets. Motivated by applications such as blind source separation and missing data imputation, this thesis also proposes efficient algorithms that make these models practical for real-world applications.

Bounded Simplex-Structured Matrix Factorization

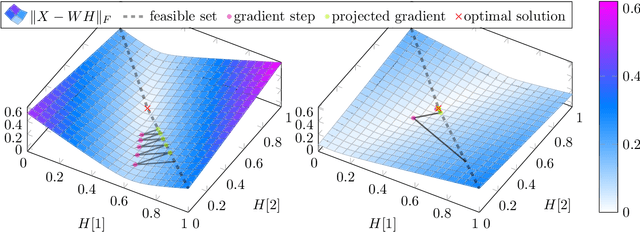
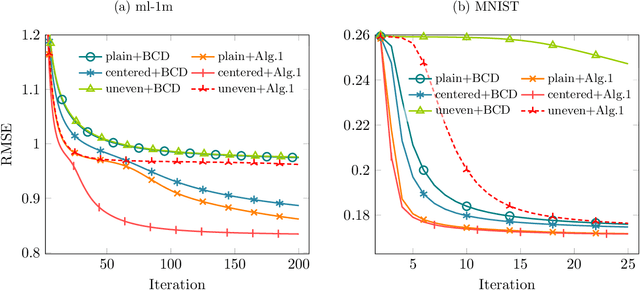
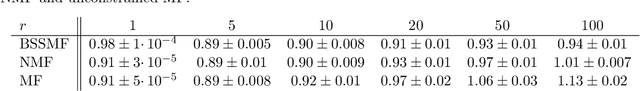
In this paper, we propose a new low-rank matrix factorization model dubbed bounded simplex-structured matrix factorization (BSSMF). Given an input matrix $X$ and a factorization rank $r$, BSSMF looks for a matrix $W$ with $r$ columns and a matrix $H$ with $r$ rows such that $X \approx WH$ where the entries in each column of $W$ are bounded, that is, they belong to given intervals, and the columns of $H$ belong to the probability simplex, that is, $H$ is column stochastic. BSSMF generalizes nonnegative matrix factorization (NMF), and simplex-structured matrix factorization (SSMF). BSSMF is particularly well suited when the entries of the input matrix $X$ belong to a given interval; for example when the rows of $X$ represent images, or $X$ is a rating matrix such as in the Netflix and MovieLens data sets where the entries of $X$ belong to the interval $[1,5]$. The simplex-structured matrix $H$ not only leads to an easily understandable decomposition providing a soft clustering of the columns of $X$, but implies that the entries of each column of $WH$ belong to the same intervals as the columns of $W$. In this paper, we first propose a fast algorithm for BSSMF, even in the presence of missing data in $X$. Then we provide identifiability conditions for BSSMF, that is, we provide conditions under which BSSMF admits a unique decomposition, up to trivial ambiguities. Finally, we illustrate the effectiveness of BSSMF on two applications: extraction of features in a set of images, and the matrix completion problem for recommender systems.