Combining Anatomical and Functional Networks for Neuropathology Identification: A Case Study on Autism Spectrum Disorder

While the prevalence of Autism Spectrum Disorder (ASD) is increasing, research towards the definition of a common etiology is still ongoing. In this regard, modern machine learning and network science pave the way for a better understanding of the pathology and the development of diagnosis aid systems. At the same time, the culture of data sharing heads favorably in that direction, with the availability of large datasets such as the Autism Brain Imaging Data Exchange (ABIDE) one. The present work addresses the classification of neurotypical and ASD subjects by combining knowledge about both the anatomy and the functional activity of the brain. In particular, we model the brain structure as a graph, and the time-varying resting-state functional MRI (rs-fMRI) signals as values that live on the nodes of that graph. We then borrow tools from the emerging field of Graph Signal Processing (GSP) to build features related to the frequency content of these signals. In order to make these features highly discriminative, we apply an extension of the Fukunaga-Koontz transform. Finally, we use these new markers to train a decision tree, an interpretable classification scheme, which results in a final diagnosis aid model. Interestingly, the resulting decision tree outperforms state-of-the-art methods on the ABIDE dataset. Moreover, the analysis of the predictive markers reveals the influence of the frontal and temporal lobes in the diagnosis of the disorder, which is in line with previous findings in the literature of neuroscience. Our results indicate that exploiting jointly structural and functional information of the brain can reveal important information about the complexity of the neuropathology.

A One-Class Decision Tree Based on Kernel Density Estimation

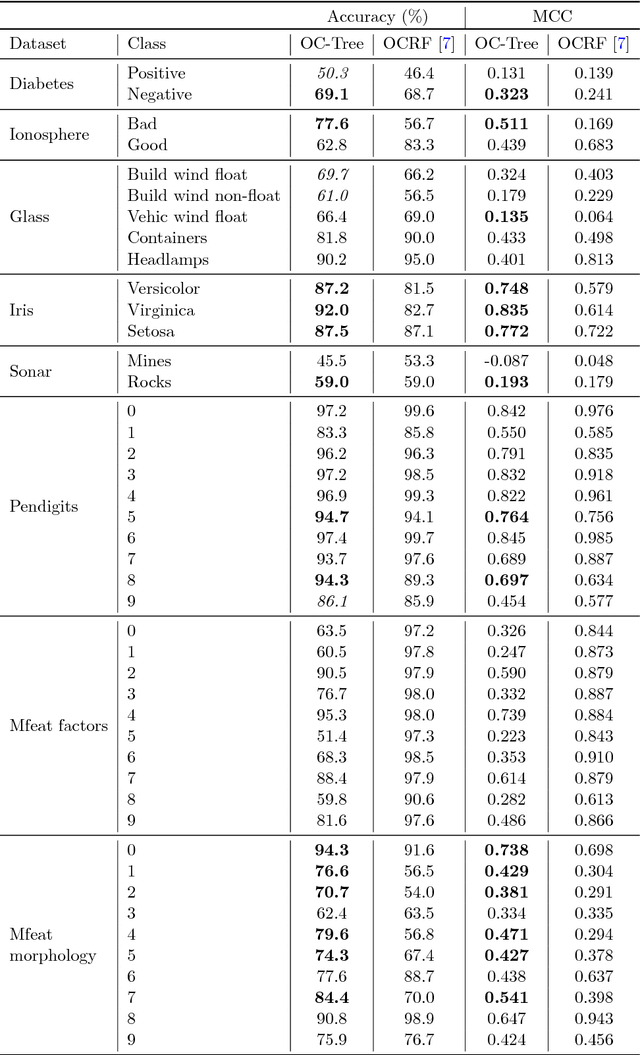
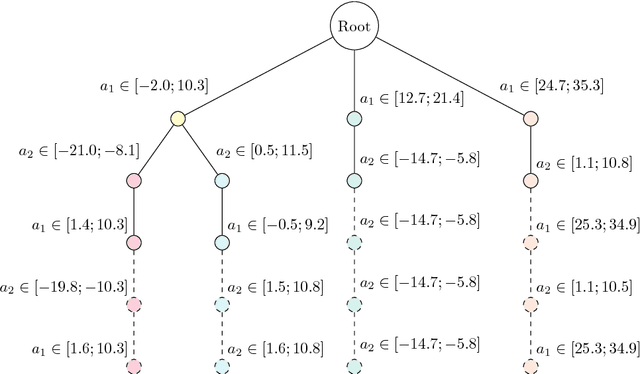
One-Class Classification (OCC) is a domain of machine learning which achieves training by means of a single class sample. The present work aims at developing a one-class model which addresses concerns of both performance and readability. To this end, we propose a hybrid OCC method which relies on density estimation as part of a tree-based learning algorithm. Within a greedy and recursive approach, our proposal rests on kernel density estimation to split a data subset on the basis of one or several intervals of interest. Our method shows favorable performance in comparison with common methods of the literature on a range of benchmark datasets.