Multi-Scale Node Embeddings for Graph Modeling and Generation

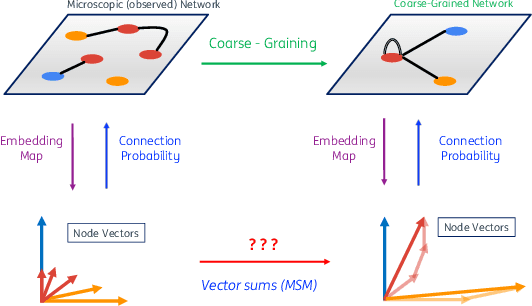
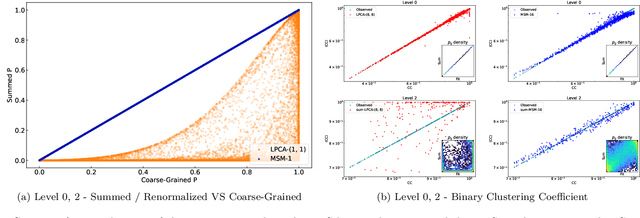
Lying at the interface between Network Science and Machine Learning, node embedding algorithms take a graph as input and encode its structure onto output vectors that represent nodes in an abstract geometric space, enabling various vector-based downstream tasks such as network modelling, data compression, link prediction, and community detection. Two apparently unrelated limitations affect these algorithms. On one hand, it is not clear what the basic operation defining vector spaces, i.e. the vector sum, corresponds to in terms of the original nodes in the network. On the other hand, while the same input network can be represented at multiple levels of resolution by coarse-graining the constituent nodes into arbitrary block-nodes, the relationship between node embeddings obtained at different hierarchical levels is not understood. Here, building on recent results in network renormalization theory, we address these two limitations at once and define a multiscale node embedding method that, upon arbitrary coarse-grainings, ensures statistical consistency of the embedding vector of a block-node with the sum of the embedding vectors of its constituent nodes. We illustrate the power of this approach on two economic networks that can be naturally represented at multiple resolution levels: namely, the international trade between (sets of) countries and the input-output flows among (sets of) industries in the Netherlands. We confirm the statistical consistency between networks retrieved from coarse-grained node vectors and networks retrieved from sums of fine-grained node vectors, a result that cannot be achieved by alternative methods. Several key network properties, including a large number of triangles, are successfully replicated already from embeddings of very low dimensionality, allowing for the generation of faithful replicas of the original networks at arbitrary resolution levels.

End-to-End Learning from Complex Multigraphs with Latent Graph Convolutional Networks

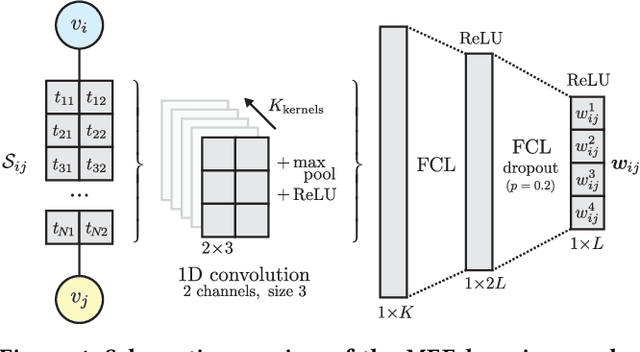
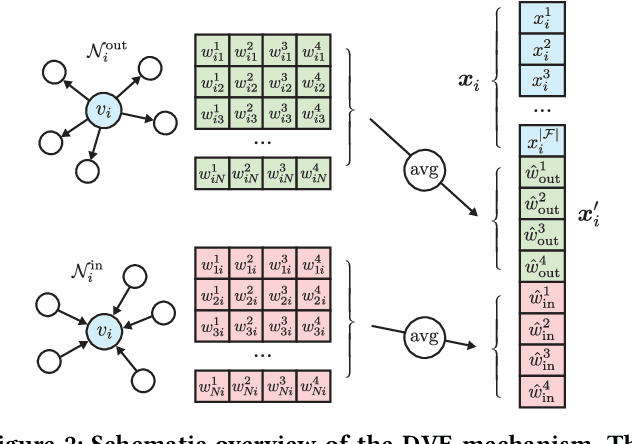
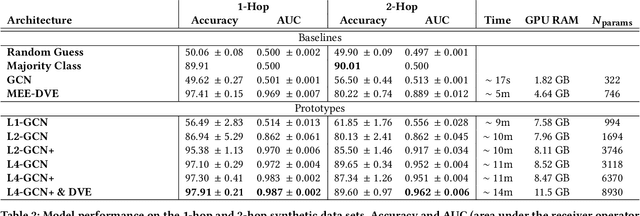
We study the problem of end-to-end learning from complex multigraphs with potentially very large numbers of edges between two vertices, each edge labeled with rich information. Examples of such graphs include financial transactions, communication networks, or flights between airports. We propose Latent-Graph Convolutional Networks (L-GCNs), which can successfully propagate information from these edge labels to a latent adjacency tensor, after which further propagation and downstream tasks can be performed, such as node classification. We evaluate the performance of several variations of the model on two synthetic datasets simulating fraud in financial transaction networks, to ensure that the model must make use of edge labels in order to achieve good classification performance. We find that allowing for nonlinear interactions on a per-neighbor basis enhances performance significantly, while also showing promising results in an inductive setting.