End-to-End Learning from Complex Multigraphs with Latent Graph Convolutional Networks
Paper and Code
Aug 14, 2019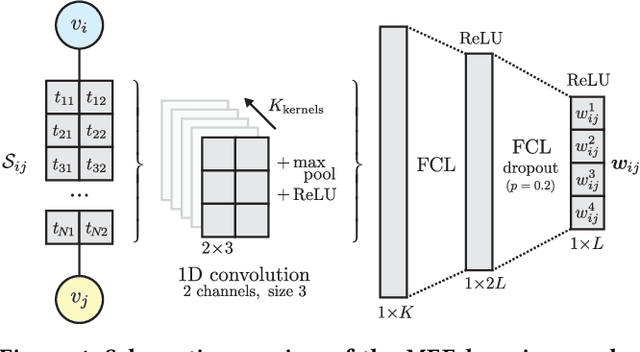

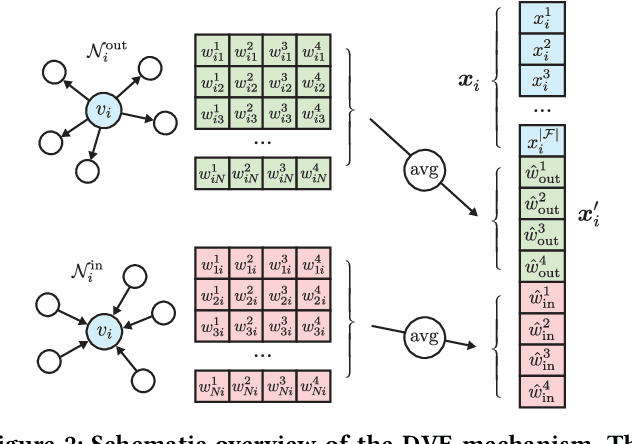
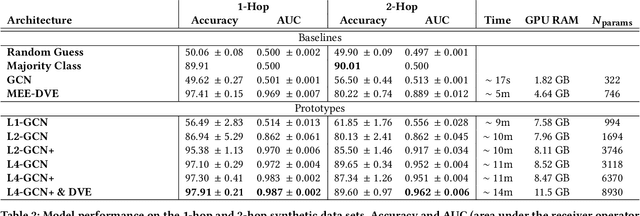
We study the problem of end-to-end learning from complex multigraphs with potentially very large numbers of edges between two vertices, each edge labeled with rich information. Examples of such graphs include financial transactions, communication networks, or flights between airports. We propose Latent-Graph Convolutional Networks (L-GCNs), which can successfully propagate information from these edge labels to a latent adjacency tensor, after which further propagation and downstream tasks can be performed, such as node classification. We evaluate the performance of several variations of the model on two synthetic datasets simulating fraud in financial transaction networks, to ensure that the model must make use of edge labels in order to achieve good classification performance. We find that allowing for nonlinear interactions on a per-neighbor basis enhances performance significantly, while also showing promising results in an inductive setting.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge