Multi-Scale Node Embeddings for Graph Modeling and Generation

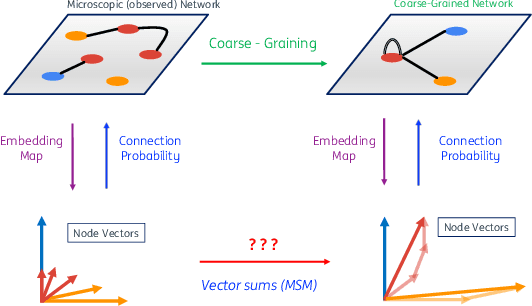
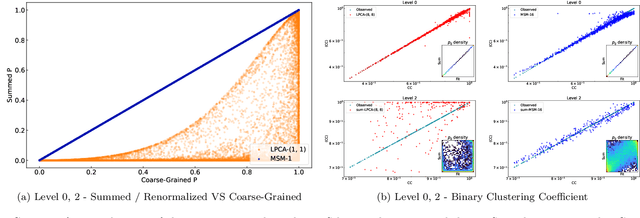
Lying at the interface between Network Science and Machine Learning, node embedding algorithms take a graph as input and encode its structure onto output vectors that represent nodes in an abstract geometric space, enabling various vector-based downstream tasks such as network modelling, data compression, link prediction, and community detection. Two apparently unrelated limitations affect these algorithms. On one hand, it is not clear what the basic operation defining vector spaces, i.e. the vector sum, corresponds to in terms of the original nodes in the network. On the other hand, while the same input network can be represented at multiple levels of resolution by coarse-graining the constituent nodes into arbitrary block-nodes, the relationship between node embeddings obtained at different hierarchical levels is not understood. Here, building on recent results in network renormalization theory, we address these two limitations at once and define a multiscale node embedding method that, upon arbitrary coarse-grainings, ensures statistical consistency of the embedding vector of a block-node with the sum of the embedding vectors of its constituent nodes. We illustrate the power of this approach on two economic networks that can be naturally represented at multiple resolution levels: namely, the international trade between (sets of) countries and the input-output flows among (sets of) industries in the Netherlands. We confirm the statistical consistency between networks retrieved from coarse-grained node vectors and networks retrieved from sums of fine-grained node vectors, a result that cannot be achieved by alternative methods. Several key network properties, including a large number of triangles, are successfully replicated already from embeddings of very low dimensionality, allowing for the generation of faithful replicas of the original networks at arbitrary resolution levels.

Inference of dynamical gene regulatory networks from single-cell data with physics informed neural networks

One of the main goals of developmental biology is to reveal the gene regulatory networks (GRNs) underlying the robust differentiation of multipotent progenitors into precisely specified cell types. Most existing methods to infer GRNs from experimental data have limited predictive power as the inferred GRNs merely reflect gene expression similarity or correlation. Here, we demonstrate, how physics-informed neural networks (PINNs) can be used to infer the parameters of predictive, dynamical GRNs that provide mechanistic understanding of biological processes. Specifically we study GRNs that exhibit bifurcation behavior and can therefore model cell differentiation. We show that PINNs outperform regular feed-forward neural networks on the parameter inference task and analyze two relevant experimental scenarios: 1. a system with cell communication for which gene expression trajectories are available and 2. snapshot measurements of a cell population in which cell communication is absent. Our analysis will inform the design of future experiments to be analyzed with PINNs and provides a starting point to explore this powerful class of neural network models further.