Eugene Demler
Correlator Convolutional Neural Networks: An Interpretable Architecture for Image-like Quantum Matter Data
Nov 06, 2020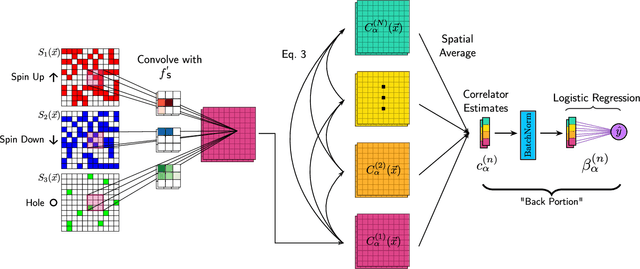
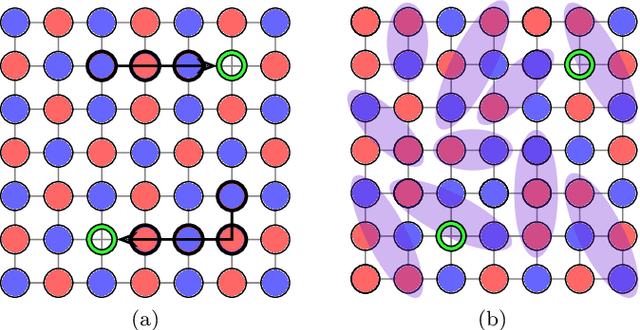
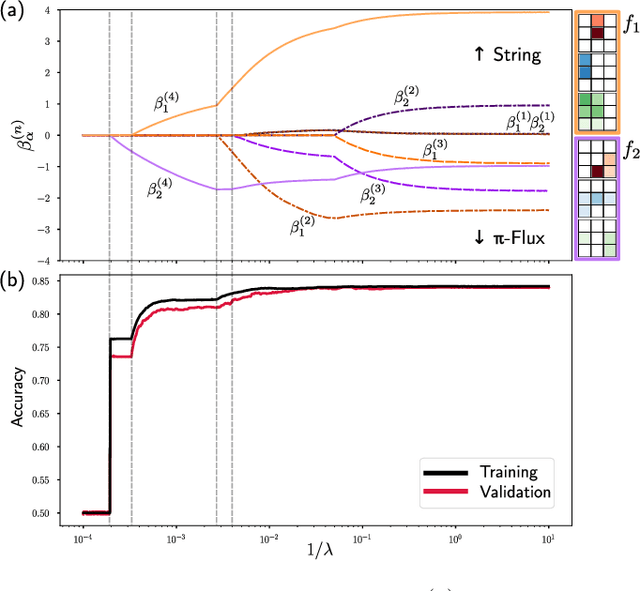
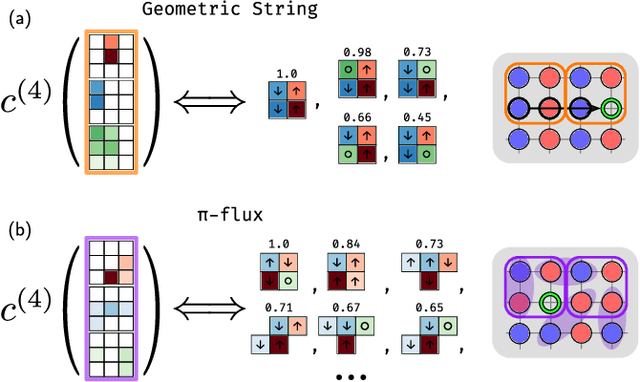
Abstract:Machine learning models are a powerful theoretical tool for analyzing data from quantum simulators, in which results of experiments are sets of snapshots of many-body states. Recently, they have been successfully applied to distinguish between snapshots that can not be identified using traditional one and two point correlation functions. Thus far, the complexity of these models has inhibited new physical insights from this approach. Here, using a novel set of nonlinearities we develop a network architecture that discovers features in the data which are directly interpretable in terms of physical observables. In particular, our network can be understood as uncovering high-order correlators which significantly differ between the data studied. We demonstrate this new architecture on sets of simulated snapshots produced by two candidate theories approximating the doped Fermi-Hubbard model, which is realized in state-of-the art quantum gas microscopy experiments. From the trained networks, we uncover that the key distinguishing features are fourth-order spin-charge correlators, providing a means to compare experimental data to theoretical predictions. Our approach lends itself well to the construction of simple, end-to-end interpretable architectures and is applicable to arbitrary lattice data, thus paving the way for new physical insights from machine learning studies of experimental as well as numerical data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge