PathFinder: Discovering Decision Pathways in Deep Neural Networks

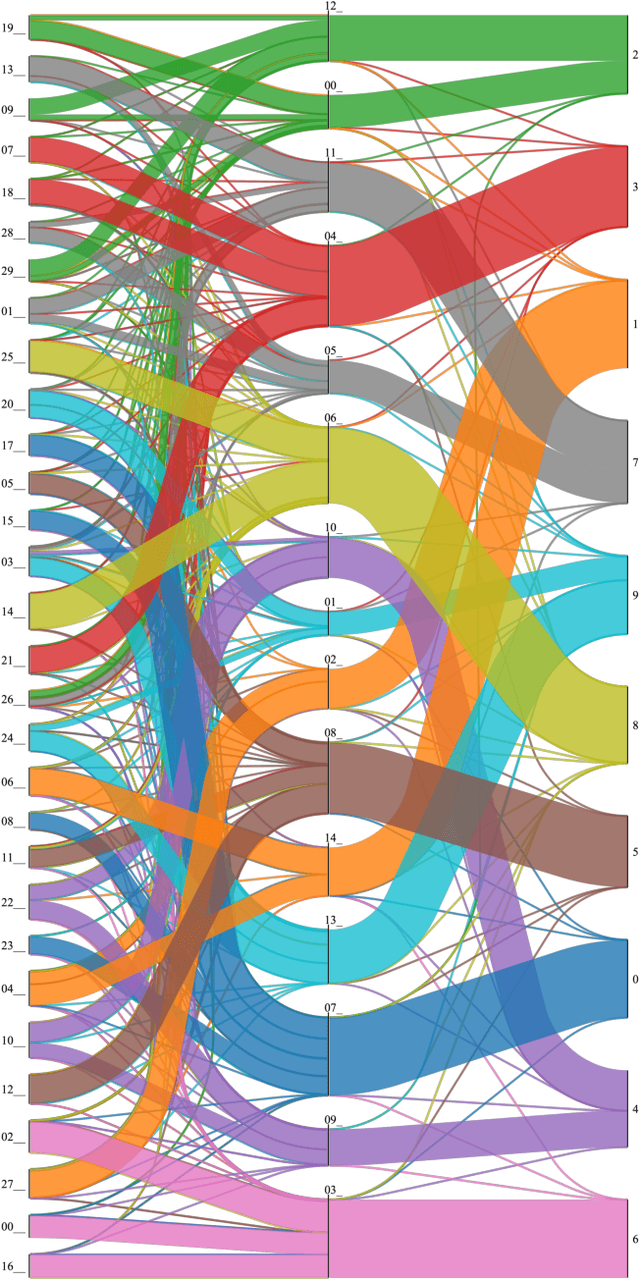
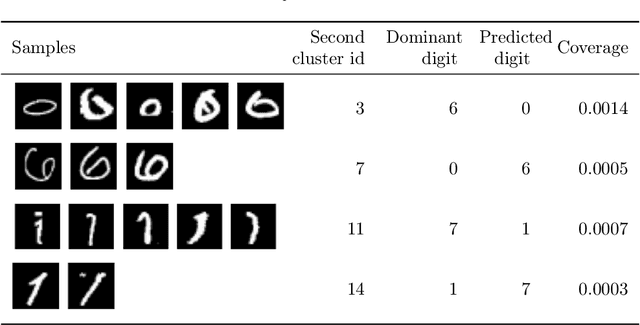
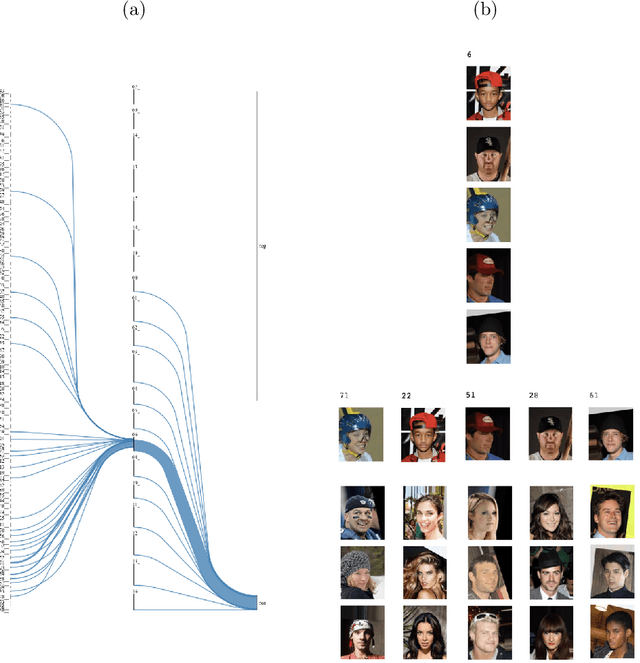
Explainability is becoming an increasingly important topic for deep neural networks. Though the operation in convolutional layers is easier to understand, processing becomes opaque in fully-connected layers. The basic idea in our work is that each instance, as it flows through the layers, causes a different activation pattern in the hidden layers and in our Paths methodology, we cluster these activation vectors for each hidden layer and then see how the clusters in successive layers connect to one another as activation flows from the input layer to the output. We find that instances of the same class follow a small number of cluster sequences over the layers, which we name ``decision paths." Such paths explain how classification decisions are typically made, and also help us determine outliers that follow unusual paths. We also propose using the Sankey diagram to visualize such pathways. We validate our method with experiments on two feed-forward networks trained on MNIST and CELEB data sets, and one recurrent network trained on PenDigits.

Hierarchical Mixtures of Generators for Adversarial Learning

Generative adversarial networks (GANs) are deep neural networks that allow us to sample from an arbitrary probability distribution without explicitly estimating the distribution. There is a generator that takes a latent vector as input and transforms it into a valid sample from the distribution. There is also a discriminator that is trained to discriminate such fake samples from true samples of the distribution; at the same time, the generator is trained to generate fakes that the discriminator cannot tell apart from the true samples. Instead of learning a global generator, a recent approach involves training multiple generators each responsible from one part of the distribution. In this work, we review such approaches and propose the hierarchical mixture of generators, inspired from the hierarchical mixture of experts model, that learns a tree structure implementing a hierarchical clustering with soft splits in the decision nodes and local generators in the leaves. Since the generators are combined softly, the whole model is continuous and can be trained using gradient-based optimization, just like the original GAN model. Our experiments on five image data sets, namely, MNIST, FashionMNIST, UTZap50K, Oxford Flowers, and CelebA, show that our proposed model generates samples of high quality and diversity in terms of popular GAN evaluation metrics. The learned hierarchical structure also leads to knowledge extraction.

Dropout Regularization in Hierarchical Mixture of Experts

Dropout is a very effective method in preventing overfitting and has become the go-to regularizer for multi-layer neural networks in recent years. Hierarchical mixture of experts is a hierarchically gated model that defines a soft decision tree where leaves correspond to experts and decision nodes correspond to gating models that softly choose between its children, and as such, the model defines a soft hierarchical partitioning of the input space. In this work, we propose a variant of dropout for hierarchical mixture of experts that is faithful to the tree hierarchy defined by the model, as opposed to having a flat, unitwise independent application of dropout as one has with multi-layer perceptrons. We show that on a synthetic regression data and on MNIST and CIFAR-10 datasets, our proposed dropout mechanism prevents overfitting on trees with many levels improving generalization and providing smoother fits.

Continuously Constructive Deep Neural Networks

Traditionally, deep learning algorithms update the network weights whereas the network architecture is chosen manually, using a process of trial and error. In this work, we propose two novel approaches that automatically update the network structure while also learning its weights. The novelty of our approach lies in our parameterization where the depth, or additional complexity, is encapsulated continuously in the parameter space through control parameters that add additional complexity. We propose two methods: In tunnel networks, this selection is done at the level of a hidden unit, and in budding perceptrons, this is done at the level of a network layer; updating this control parameter introduces either another hidden unit or another hidden layer. We show the effectiveness of our methods on the synthetic two-spirals data and on two real data sets of MNIST and MIRFLICKR, where we see that our proposed methods, with the same set of hyperparameters, can correctly adjust the network complexity to the task complexity.

Distributed Decision Trees

Recently proposed budding tree is a decision tree algorithm in which every node is part internal node and part leaf. This allows representing every decision tree in a continuous parameter space, and therefore a budding tree can be jointly trained with backpropagation, like a neural network. Even though this continuity allows it to be used in hierarchical representation learning, the learned representations are local: Activation makes a soft selection among all root-to-leaf paths in a tree. In this work we extend the budding tree and propose the distributed tree where the children use different and independent splits and hence multiple paths in a tree can be traversed at the same time. This ability to combine multiple paths gives the power of a distributed representation, as in a traditional perceptron layer. We show that distributed trees perform comparably or better than budding and traditional hard trees on classification and regression tasks.

Autoencoder Trees

We discuss an autoencoder model in which the encoding and decoding functions are implemented by decision trees. We use the soft decision tree where internal nodes realize soft multivariate splits given by a gating function and the overall output is the average of all leaves weighted by the gating values on their path. The encoder tree takes the input and generates a lower dimensional representation in the leaves and the decoder tree takes this and reconstructs the original input. Exploiting the continuity of the trees, autoencoder trees are trained with stochastic gradient descent. On handwritten digit and news data, we see that the autoencoder trees yield good reconstruction error compared to traditional autoencoder perceptrons. We also see that the autoencoder tree captures hierarchical representations at different granularities of the data on its different levels and the leaves capture the localities in the input space.