Towards Characterizing Divergence in Deep Q-Learning

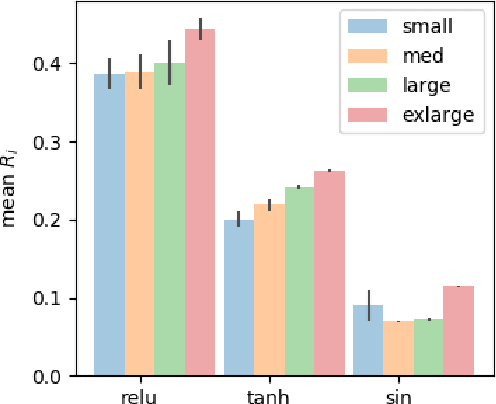
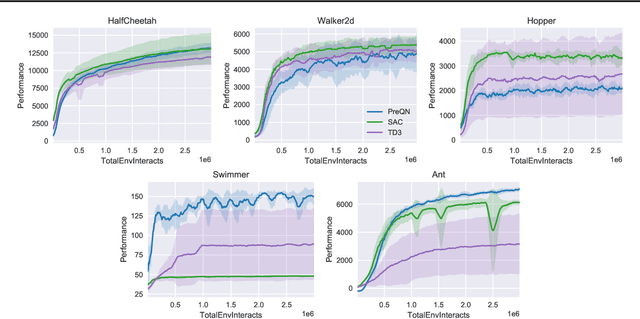
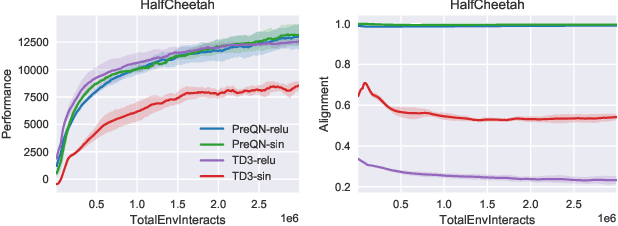
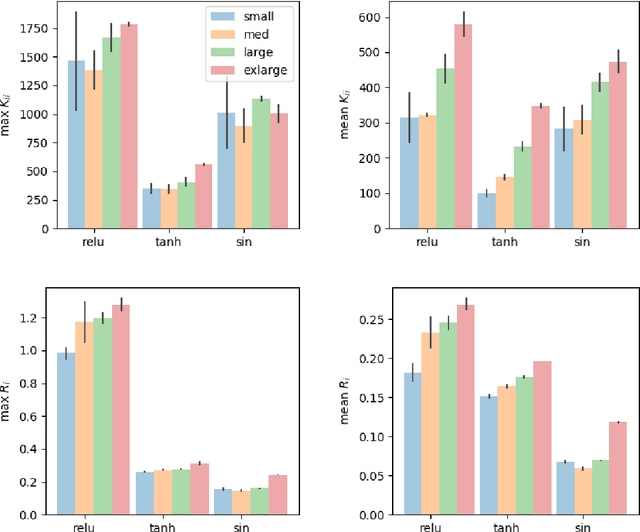
Deep Q-Learning (DQL), a family of temporal difference algorithms for control, employs three techniques collectively known as the `deadly triad' in reinforcement learning: bootstrapping, off-policy learning, and function approximation. Prior work has demonstrated that together these can lead to divergence in Q-learning algorithms, but the conditions under which divergence occurs are not well-understood. In this note, we give a simple analysis based on a linear approximation to the Q-value updates, which we believe provides insight into divergence under the deadly triad. The central point in our analysis is to consider when the leading order approximation to the deep-Q update is or is not a contraction in the sup norm. Based on this analysis, we develop an algorithm which permits stable deep Q-learning for continuous control without any of the tricks conventionally used (such as target networks, adaptive gradient optimizers, or using multiple Q functions). We demonstrate that our algorithm performs above or near state-of-the-art on standard MuJoCo benchmarks from the OpenAI Gym.

Natural Gradient Deep Q-learning

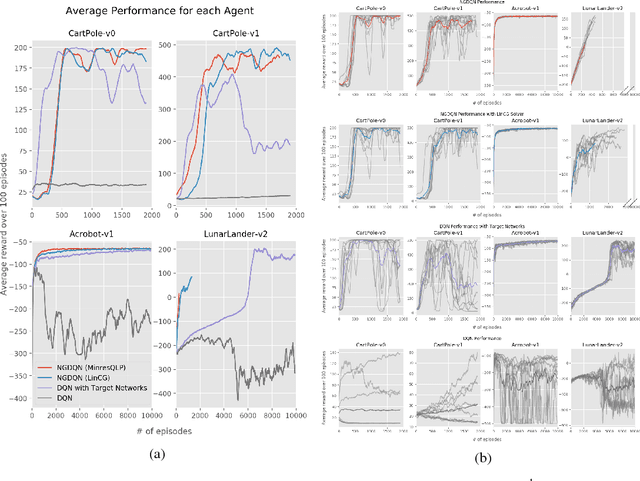
This paper presents findings for training a Q-learning reinforcement learning agent using natural gradient techniques. We compare the original deep Q-network (DQN) algorithm to its natural gradient counterpart (NGDQN), measuring NGDQN and DQN performance on classic controls environments without target networks. We find that NGDQN performs favorably relative to DQN, converging to significantly better policies faster and more frequently. These results indicate that natural gradient could be used for value function optimization in reinforcement learning to accelerate and stabilize training.