A Theoretical and Empirical Taxonomy of Imbalance in Binary Classification

Class imbalance significantly degrades classification performance, yet its effects are rarely analyzed from a unified theoretical perspective. We propose a principled framework based on three fundamental scales: the imbalance coefficient $η$, the sample--dimension ratio $κ$, and the intrinsic separability $Δ$. Starting from the Gaussian Bayes classifier, we derive closed-form Bayes errors and show how imbalance shifts the discriminant boundary, yielding a deterioration slope that predicts four regimes: Normal, Mild, Extreme, and Catastrophic. Using a balanced high-dimensional genomic dataset, we vary only $η$ while keeping $κ$ and $Δ$ fixed. Across parametric and non-parametric models, empirical degradation closely follows theoretical predictions: minority Recall collapses once $\log(η)$ exceeds $Δ\sqrtκ$, Precision increases asymmetrically, and F1-score and PR-AUC decline in line with the predicted regimes. These results show that the triplet $(η,κ,Δ)$ provides a model-agnostic, geometrically grounded explanation of imbalance-induced deterioration.

Fibonacci-Driven Recursive Ensembles: Algorithms, Convergence, and Learning Dynamics

This paper develops the algorithmic and dynamical foundations of recursive ensemble learning driven by Fibonacci-type update flows. In contrast with classical boosting Freund and Schapire (1997); Friedman (2001), where the ensemble evolves through first-order additive updates, we study second-order recursive architectures in which each predictor depends on its two immediate predecessors. These Fibonacci flows induce a learning dynamic with memory, allowing ensembles to integrate past structure while adapting to new residual information. We introduce a general family of recursive weight-update algorithms encompassing Fibonacci, tribonacci, and higher-order recursions, together with continuous-time limits that yield systems of differential equations governing ensemble evolution. We establish global convergence conditions, spectral stability criteria, and non-asymptotic generalization bounds under Rademacher Bartlett and Mendelson (2002) and algorithmic stability analyses. The resulting theory unifies recursive ensembles, structured weighting, and dynamical systems viewpoints in statistical learning. Experiments with kernel ridge regression Rasmussen and Williams (2006), spline smoothers Wahba (1990), and random Fourier feature models Rahimi and Recht (2007) demonstrate that recursive flows consistently improve approximation and generalization beyond static weighting. These results complete the trilogy begun in Papers I and II: from Fibonacci weighting, through geometric weighting theory, to fully dynamical recursive ensemble learning systems.

A General Weighting Theory for Ensemble Learning: Beyond Variance Reduction via Spectral and Geometric Structure

Ensemble learning is traditionally justified as a variance-reduction strategy, explaining its strong performance for unstable predictors such as decision trees. This explanation, however, does not account for ensembles constructed from intrinsically stable estimators-including smoothing splines, kernel ridge regression, Gaussian process regression, and other regularized reproducing kernel Hilbert space (RKHS) methods whose variance is already tightly controlled by regularization and spectral shrinkage. This paper develops a general weighting theory for ensemble learning that moves beyond classical variance-reduction arguments. We formalize ensembles as linear operators acting on a hypothesis space and endow the space of weighting sequences with geometric and spectral constraints. Within this framework, we derive a refined bias-variance approximation decomposition showing how non-uniform, structured weights can outperform uniform averaging by reshaping approximation geometry and redistributing spectral complexity, even when variance reduction is negligible. Our main results provide conditions under which structured weighting provably dominates uniform ensembles, and show that optimal weights arise as solutions to constrained quadratic programs. Classical averaging, stacking, and recently proposed Fibonacci-based ensembles appear as special cases of this unified theory, which further accommodates geometric, sub-exponential, and heavy-tailed weighting laws. Overall, the work establishes a principled foundation for structure-driven ensemble learning, explaining why ensembles remain effective for smooth, low-variance base learners and setting the stage for distribution-adaptive and dynamically evolving weighting schemes developed in subsequent work.

On Fibonacci Ensembles: An Alternative Approach to Ensemble Learning Inspired by the Timeless Architecture of the Golden Ratio

Nature rarely reveals her secrets bluntly, yet in the Fibonacci sequence she grants us a glimpse of her quiet architecture of growth, harmony, and recursive stability \citep{Koshy2001Fibonacci, Livio2002GoldenRatio}. From spiral galaxies to the unfolding of leaves, this humble sequence reflects a universal grammar of balance. In this work, we introduce \emph{Fibonacci Ensembles}, a mathematically principled yet philosophically inspired framework for ensemble learning that complements and extends classical aggregation schemes such as bagging, boosting, and random forests \citep{Breiman1996Bagging, Breiman2001RandomForests, Friedman2001GBM, Zhou2012Ensemble, HastieTibshiraniFriedman2009ESL}. Two intertwined formulations unfold: (1) the use of normalized Fibonacci weights -- tempered through orthogonalization and Rao--Blackwell optimization -- to achieve systematic variance reduction among base learners, and (2) a second-order recursive ensemble dynamic that mirrors the Fibonacci flow itself, enriching representational depth beyond classical boosting. The resulting methodology is at once rigorous and poetic: a reminder that learning systems flourish when guided by the same intrinsic harmonies that shape the natural world. Through controlled one-dimensional regression experiments using both random Fourier feature ensembles \citep{RahimiRecht2007RFF} and polynomial ensembles, we exhibit regimes in which Fibonacci weighting matches or improves upon uniform averaging and interacts in a principled way with orthogonal Rao--Blackwellization. These findings suggest that Fibonacci ensembles form a natural and interpretable design point within the broader theory of ensemble learning.

No Intelligence Without Statistics: The Invisible Backbone of Artificial Intelligence

The rapid ascent of artificial intelligence (AI) is often portrayed as a revolution born from computer science and engineering. This narrative, however, obscures a fundamental truth: the theoretical and methodological core of AI is, and has always been, statistical. This paper systematically argues that the field of statistics provides the indispensable foundation for machine learning and modern AI. We deconstruct AI into nine foundational pillars-Inference, Density Estimation, Sequential Learning, Generalization, Representation Learning, Interpretability, Causality, Optimization, and Unification-demonstrating that each is built upon century-old statistical principles. From the inferential frameworks of hypothesis testing and estimation that underpin model evaluation, to the density estimation roots of clustering and generative AI; from the time-series analysis inspiring recurrent networks to the causal models that promise true understanding, we trace an unbroken statistical lineage. While celebrating the computational engines that power modern AI, we contend that statistics provides the brain-the theoretical frameworks, uncertainty quantification, and inferential goals-while computer science provides the brawn-the scalable algorithms and hardware. Recognizing this statistical backbone is not merely an academic exercise, but a necessary step for developing more robust, interpretable, and trustworthy intelligent systems. We issue a call to action for education, research, and practice to re-embrace this statistical foundation. Ignoring these roots risks building a fragile future; embracing them is the path to truly intelligent machines. There is no machine learning without statistical learning; no artificial intelligence without statistical thought.

Towards AI-Driven Policing: Interdisciplinary Knowledge Discovery from Police Body-Worn Camera Footage

This paper proposes a novel interdisciplinary framework for analyzing police body-worn camera (BWC) footage from the Rochester Police Department (RPD) using advanced artificial intelligence (AI) and statistical machine learning (ML) techniques. Our goal is to detect, classify, and analyze patterns of interaction between police officers and civilians to identify key behavioral dynamics, such as respect, disrespect, escalation, and de-escalation. We apply multimodal data analysis by integrating video, audio, and natural language processing (NLP) techniques to extract meaningful insights from BWC footage. We present our methodology, computational techniques, and findings, outlining a practical approach for law enforcement while advancing the frontiers of knowledge discovery from police BWC data.

Emerging Statistical Machine Learning Techniques for Extreme Temperature Forecasting in U.S. Cities

In this paper, we present a comprehensive analysis of extreme temperature patterns using emerging statistical machine learning techniques. Our research focuses on exploring and comparing the effectiveness of various statistical models for climate time series forecasting. The models considered include Auto-Regressive Integrated Moving Average, Exponential Smoothing, Multilayer Perceptrons, and Gaussian Processes. We apply these methods to climate time series data from five most populated U.S. cities, utilizing Python and Julia to demonstrate the role of statistical computing in understanding climate change and its impacts. Our findings highlight the differences between the statistical methods and identify Multilayer Perceptrons as the most effective approach. Additionally, we project extreme temperatures using this best-performing method, up to 2030, and examine whether the temperature changes are greater than zero, thereby testing a hypothesis.

Efficient Novelty Detection Methods for Early Warning of Potential Fatal Diseases

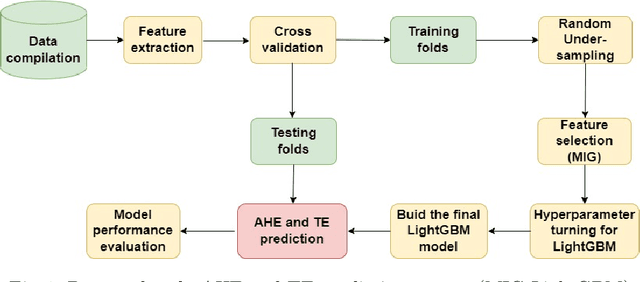
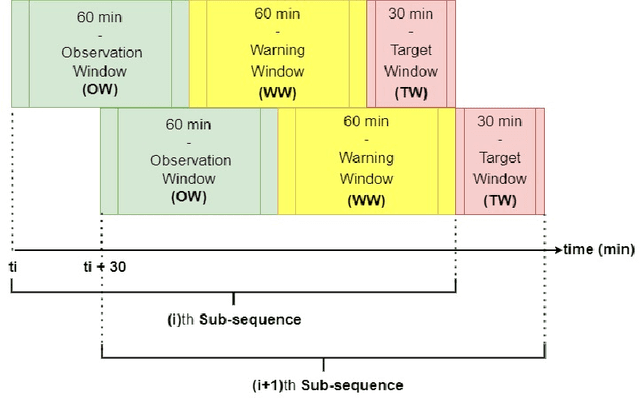
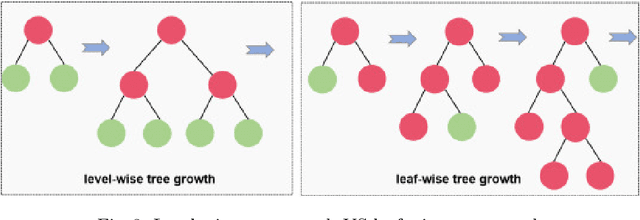
Fatal diseases, as Critical Health Episodes (CHEs), represent real dangers for patients hospitalized in Intensive Care Units. These episodes can lead to irreversible organ damage and death. Nevertheless, diagnosing them in time would greatly reduce their inconvenience. This study therefore focused on building a highly effective early warning system for CHEs such as Acute Hypotensive Episodes and Tachycardia Episodes. To facilitate the precocity of the prediction, a gap of one hour was considered between the observation periods (Observation Windows) and the periods during which a critical event can occur (Target Windows). The MIMIC II dataset was used to evaluate the performance of the proposed system. This system first includes extracting additional features using three different modes. Then, the feature selection process allowing the selection of the most relevant features was performed using the Mutual Information Gain feature importance. Finally, the high-performance predictive model LightGBM was used to perform episode classification. This approach called MIG-LightGBM was evaluated using five different metrics: Event Recall (ER), Reduced Precision (RP), average Anticipation Time (aveAT), average False Alarms (aveFA), and Event F1-score (EF1-score). A method is therefore considered highly efficient for the early prediction of CHEs if it exhibits not only a large aveAT but also a large EF1-score and a low aveFA. Compared to systems using Extreme Gradient Boosting, Support Vector Classification or Naive Bayes as a predictive model, the proposed system was found to be highly dominant. It also confirmed its superiority over the Layered Learning approach.

Boosting the Predictive Accurary of Singer Identification Using Discrete Wavelet Transform For Feature Extraction

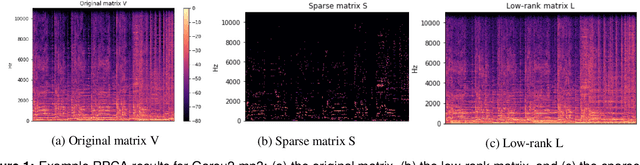
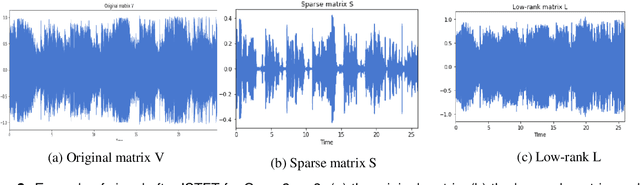
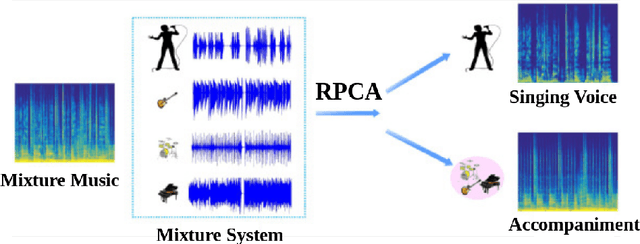
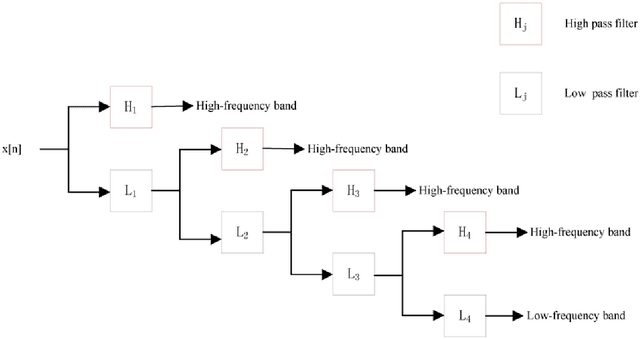
Facing the diversity and growth of the musical field nowadays, the search for precise songs becomes more and more complex. The identity of the singer facilitates this search. In this project, we focus on the problem of identifying the singer by using different methods for feature extraction. Particularly, we introduce the Discrete Wavelet Transform (DWT) for this purpose. To the best of our knowledge, DWT has never been used this way before in the context of singer identification. This process consists of three crucial parts. First, the vocal signal is separated from the background music by using the Robust Principal Component Analysis (RPCA). Second, features from the obtained vocal signal are extracted. Here, the goal is to study the performance of the Discrete Wavelet Transform (DWT) in comparison to the Mel Frequency Cepstral Coefficient (MFCC) which is the most used technique in audio signals. Finally, we proceed with the identification of the singer where two methods have experimented: the Support Vector Machine (SVM), and the Gaussian Mixture Model (GMM). We conclude that, for a dataset of 4 singers and 200 songs, the best identification system consists of the DWT (db4) feature extraction introduced in this work combined with a linear support vector machine for identification resulting in a mean accuracy of 83.96%.

A Novel Use of Discrete Wavelet Transform Features in the Prediction of Epileptic Seizures from EEG Data

This paper demonstrates the predictive superiority of discrete wavelet transform (DWT) over previously used methods of feature extraction in the diagnosis of epileptic seizures from EEG data. Classification accuracy, specificity, and sensitivity are used as evaluation metrics. We specifically show the immense potential of 2 combinations (DWT-db4 combined with SVM and DWT-db2 combined with RF) as compared to others when it comes to diagnosing epileptic seizures either in the balanced or the imbalanced dataset. The results also highlight that MFCC performs less than all the DWT used in this study and that, The mean-differences are statistically significant respectively in the imbalanced and balanced dataset. Finally, either in the balanced or the imbalanced dataset, the feature extraction techniques, the models, and the interaction between them have a statistically significant effect on the classification accuracy.