Learning the Information Divergence

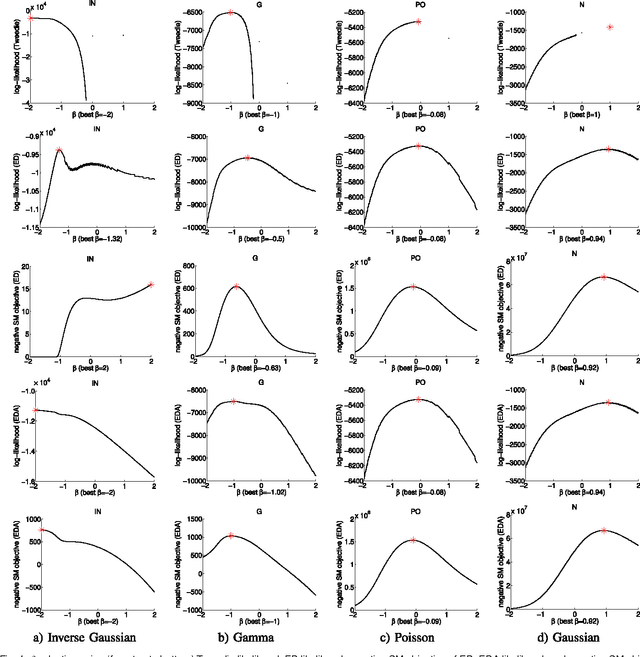
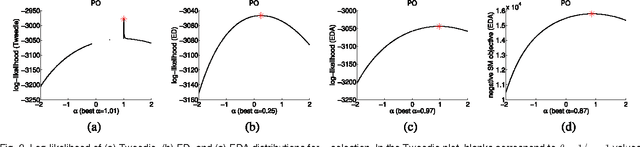
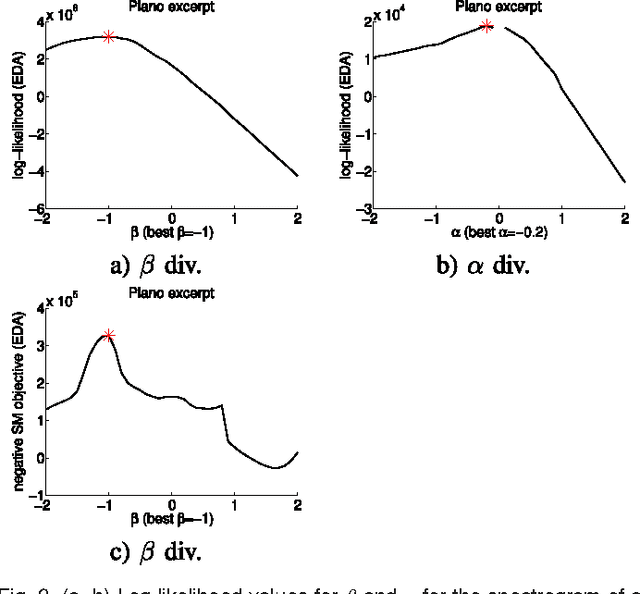
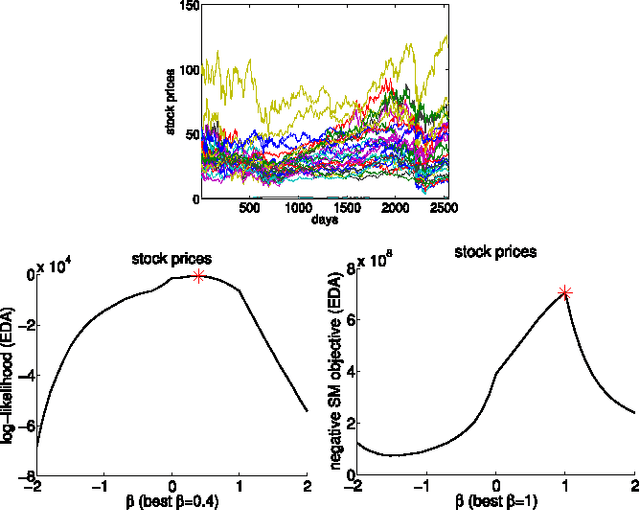
Information divergence that measures the difference between two nonnegative matrices or tensors has found its use in a variety of machine learning problems. Examples are Nonnegative Matrix/Tensor Factorization, Stochastic Neighbor Embedding, topic models, and Bayesian network optimization. The success of such a learning task depends heavily on a suitable divergence. A large variety of divergences have been suggested and analyzed, but very few results are available for an objective choice of the optimal divergence for a given task. Here we present a framework that facilitates automatic selection of the best divergence among a given family, based on standard maximum likelihood estimation. We first propose an approximated Tweedie distribution for the beta-divergence family. Selecting the best beta then becomes a machine learning problem solved by maximum likelihood. Next, we reformulate alpha-divergence in terms of beta-divergence, which enables automatic selection of alpha by maximum likelihood with reuse of the learning principle for beta-divergence. Furthermore, we show the connections between gamma and beta-divergences as well as R\'enyi and alpha-divergences, such that our automatic selection framework is extended to non-separable divergences. Experiments on both synthetic and real-world data demonstrate that our method can quite accurately select information divergence across different learning problems and various divergence families.

Clustering by Low-Rank Doubly Stochastic Matrix Decomposition

Clustering analysis by nonnegative low-rank approximations has achieved remarkable progress in the past decade. However, most approximation approaches in this direction are still restricted to matrix factorization. We propose a new low-rank learning method to improve the clustering performance, which is beyond matrix factorization. The approximation is based on a two-step bipartite random walk through virtual cluster nodes, where the approximation is formed by only cluster assigning probabilities. Minimizing the approximation error measured by Kullback-Leibler divergence is equivalent to maximizing the likelihood of a discriminative model, which endows our method with a solid probabilistic interpretation. The optimization is implemented by a relaxed Majorization-Minimization algorithm that is advantageous in finding good local minima. Furthermore, we point out that the regularized algorithm with Dirichlet prior only serves as initialization. Experimental results show that the new method has strong performance in clustering purity for various datasets, especially for large-scale manifold data.