Learning the Information Divergence
Paper and Code
Jun 05, 2014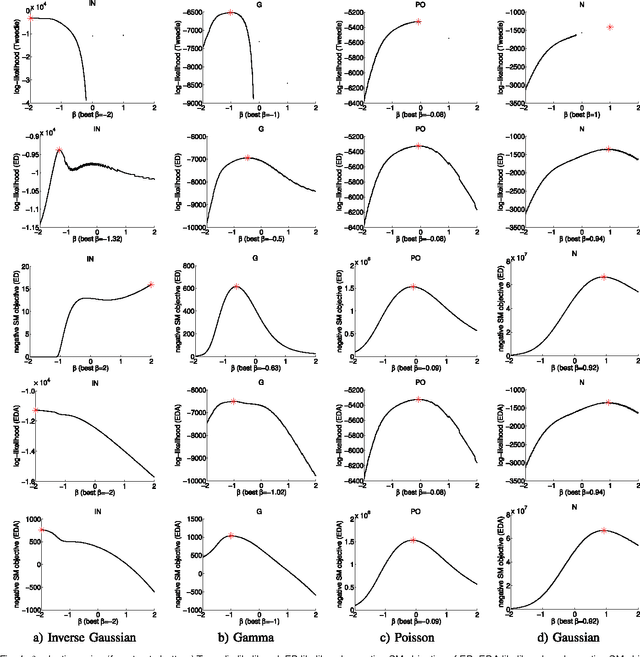
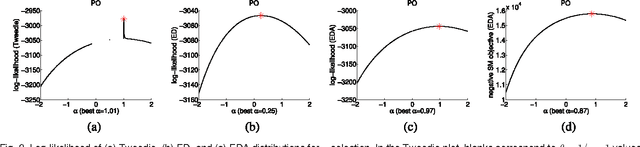
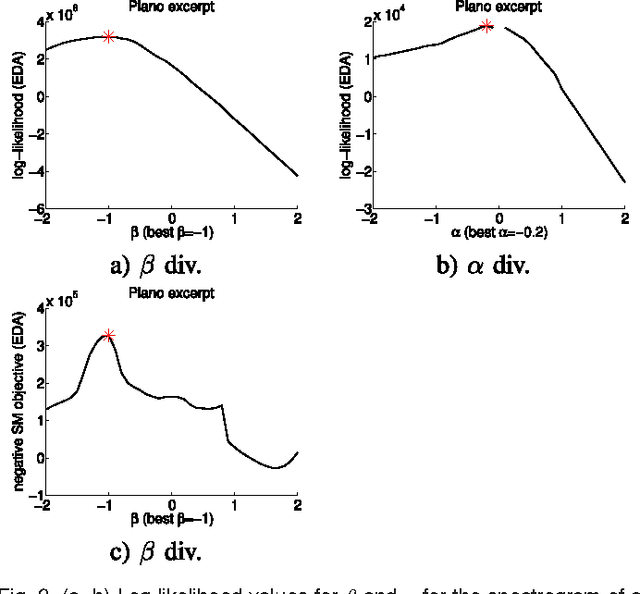
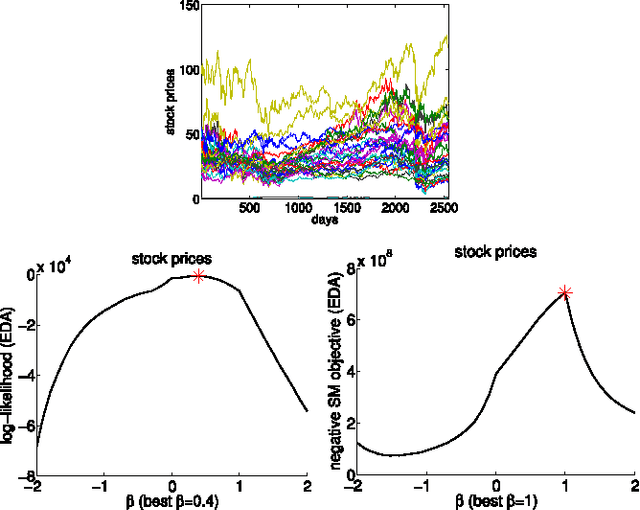
Information divergence that measures the difference between two nonnegative matrices or tensors has found its use in a variety of machine learning problems. Examples are Nonnegative Matrix/Tensor Factorization, Stochastic Neighbor Embedding, topic models, and Bayesian network optimization. The success of such a learning task depends heavily on a suitable divergence. A large variety of divergences have been suggested and analyzed, but very few results are available for an objective choice of the optimal divergence for a given task. Here we present a framework that facilitates automatic selection of the best divergence among a given family, based on standard maximum likelihood estimation. We first propose an approximated Tweedie distribution for the beta-divergence family. Selecting the best beta then becomes a machine learning problem solved by maximum likelihood. Next, we reformulate alpha-divergence in terms of beta-divergence, which enables automatic selection of alpha by maximum likelihood with reuse of the learning principle for beta-divergence. Furthermore, we show the connections between gamma and beta-divergences as well as R\'enyi and alpha-divergences, such that our automatic selection framework is extended to non-separable divergences. Experiments on both synthetic and real-world data demonstrate that our method can quite accurately select information divergence across different learning problems and various divergence families.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge